题目内容
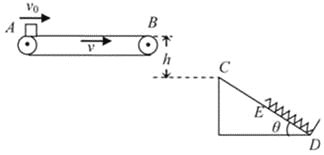
【题目】下图为火车站装载货物的示意图，AB段是距水平传送带装置高为H=5m的光滑斜面，水平段BC使用水平传送带装置，BC长L=8m，与货物包的摩擦系数为μ=0．6，皮带轮的半径为R=0．2m，上部距车厢底水平面的高度h=0．45m。设货物由静止开始从A点下滑，经过B点的拐角处无能量损失。通过调整皮带轮（不打滑）的转动角速度ω可使货物经C点被水平抛出后落在车厢上的不同位置（车厢足够长，货物不会撞到车厢壁），取g=10m/s2。
（1）当皮带轮静止时，请判断货物包能否在C点被水平抛出。若不能，请说明理由；若能，请算出货物包在车厢内的落地点到C点的水平距离；
（2）当皮带轮以角速度ω="20" rad/s顺时针匀速转动时，求货物包在车厢内的落地点到C点的水平距离；
（3）讨论货物包在车厢内的落地点到C点的水平距离s与皮带轮转动的角速度ω（顺时针匀速转动）之间的关系。
【答案】（1）0．6m（2）1．2m（3）见解析
【解析】试题分析：（1）设到达B点速度为V0，由
，得：v0=10m/s
货物从B到C做匀减速运动，
设到达C点速度为VC，由
，
得：v C="2" m/s
若刚好被水平抛出，由
得：
m/s＜2 m/s，故能被水平抛出
平抛过程，由
得：
落地点到C点的水平距离：
（2）皮带速度V皮="ωR=4" m/s
由（1）可知：货物先减速后匀速，从C点抛出的速度为VC="4" m/s
（3）Ⅰ、若货物在BC间全程减速，则有VC="2" m/s，S=0．6m，即：当0≤ω≤10 rad/s时， S=0．6m
Ⅱ、若货物在BC间全程加速，则有
，
得：vC="14" m/s，S=vc·t =4．2m
即：当ω≥70 rad/s时， S=4．2m
Ⅲ、当10＜ω＜70 rad/s时，S=ωR·t=0．06 ω
落地点到C点的水平距离：
