��Ŀ����
����Ŀ����ͼ����������Ϊm��С��ͨ����ΪL�IJ����쳤����ˮƽ��������ijһ�ߴ��������䣬���������������ˮƽ��ֱ״̬��������h�߶�ʱ�����е�����ˮƽ���õĹ⻬����O���������ٶ�Ϊg������ ��
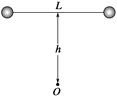
A�������붤���������˲�䣬С��ļ��ٶȴ�СΪg
B���������붤��������С��յ�����͵�Ĺ��̣������Ĺ���һֱ��С
C��С��յ�����͵�ʱ�ٶȴ�СΪ![]()
D��С��յ�����͵�ʱ�����Ӷ�С���������СΪ![]()
���𰸡�D
��������
��������������붤���������˲�䣬С������ֱ���µ��ٶȣ���ʱС����Բ���˶�����С�����������������������ã�����С��ļ��ٶȴ�С��Ϊg�����Ǵ���g������ѡ��A�����������붤��������С��յ�����͵�Ĺ��̣�С������ֱ������ٶȲ������������ȱ����С�����С����ٶȷ���Ϊˮƽ������ֱ������ٶ�Ϊ0���������Ĺ���Ӧ����������С��ѡ��B����С�����䵽��͵�Ĺ����У��ɻ�е���غ��֪��2mg��h+L/2��=2��![]() mv2���ʽ��С��յ�����͵�ʱ�ٶȴ�СΪv=
mv2���ʽ��С��յ�����͵�ʱ�ٶȴ�СΪv=![]() ����ѡ��C��������͵㣬��ţ�ٵڶ����ɿɵ�F��mg=m
����ѡ��C��������͵㣬��ţ�ٵڶ����ɿɵ�F��mg=m![]() ��������Ӷ�С���������СΪF=
��������Ӷ�С���������СΪF=![]() +3mg��ѡ��D��ȷ��
+3mg��ѡ��D��ȷ��

��ϰ��ϵ�д�
�����Ŀ