题目内容
【题目】某器件由图甲所示的玻璃圆柱体和顶角为120°的倒立玻璃圆锥体构成,圆柱和圆锥的中心轴重合,二者底面半径均为![]() a,圆柱体高为a。器件置于水平桌面上方,其截面如图乙,圆锥顶点O与桌面的距离为4a,圆锥轴线与桌面垂直。现让一半径也为
a,圆柱体高为a。器件置于水平桌面上方,其截面如图乙,圆锥顶点O与桌面的距离为4a,圆锥轴线与桌面垂直。现让一半径也为![]() a的圆柱形平行光束垂直入射到圆柱体的底面上,且使光束的中心轴与圆锥的轴重合。已知该玻璃的折射率n=
a的圆柱形平行光束垂直入射到圆柱体的底面上,且使光束的中心轴与圆锥的轴重合。已知该玻璃的折射率n=![]() ,光在真空中的速度为c。求:
,光在真空中的速度为c。求:
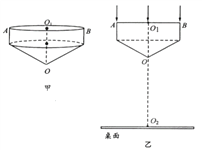
(i)从圆柱体的底面中心O1入射的光穿过玻璃器件所需时间;
(i)光束在桌面上形成的光斑的面积。
【答案】(1)![]() (2)
(2)![]()
【解析】解:如图所示,入射光沿直线经![]() 、
、![]() 、
、![]() 从圆锥的轴线射出达到桌面上
从圆锥的轴线射出达到桌面上
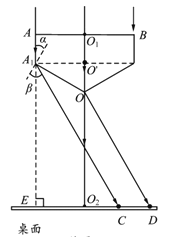
在![]() 中:
中:![]()
![]()
又![]()
光在玻璃器件中传播的时间![]()
联立解得![]()
光射到OA1界面的入射角![]() ,则
,则![]() ,故入射光线能从圆锥侧面射出,
,故入射光线能从圆锥侧面射出,
设折射角为![]() ,无限接近A点的折射光线为AC,根据折射定律有:
,无限接近A点的折射光线为AC,根据折射定律有:![]()
计算得出:![]()
过O点作![]() ,则
,则![]()
在![]() 中,
中,![]()
在![]() 中,
中, ![]()
故![]()
光束在桌面上形成光环的面积![]()

练习册系列答案
相关题目