题目内容
一个光滑的圆锥体固定在水平面桌面上，其轴线沿铅直方向，母线与轴线之间夹角θ=30度。一条长度为L的绳子（质量不计），一端的位置固定在圆锥体的顶点O处，另一端拴着一个质量为m的小物体（物体可看作质点）。物体以速率v绕圆锥体的轴线做水平匀速圆周运动。求：1）当V=2√(gL/6) 时，绳对物体的拉力；2）当V=2√(3gL/2)时，绳对物体的拉力。
小球是不是和圆锥面接触，有没有弹力，是首先要考虑的。 （1）先研究接触但没有弹力的情况，求得当时的速度。合力做向心力 mgtan30°=mv０^2/(Lsin30°) 解得V０=2√(gL/(2×2√３) ）（２）比较V和V0的大小可知第一种情况圆锥面对球有弹力，第二种情况小球以脱离圆锥面第一种：（V=2√(gL/6)）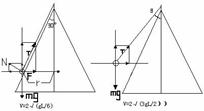 
应用正交分解 水平：Tsin30°-Ncos30°=mv^2/(Lsin30°)竖直：Tcos30°+Nsin30°=mg解得T=（1/6+（2√3）/2）mg第二种：（V=2√(3gL/2））水平：Tsinθ=mv^2/(Lsinθ)竖直：Tcosθ=mg 解得T=(3/4±（2√17）/4）mg
应用正交分解 水平：Tsin30°-Ncos30°=mv^2/(Lsin30°)竖直：Tcos30°+Nsin30°=mg解得T=（1/6+（2√3）/2）mg第二种：（V=2√(3gL/2））水平：Tsinθ=mv^2/(Lsinθ)竖直：Tcosθ=mg 解得T=(3/4±（2√17）/4）mg 
练习册系列答案
相关题目
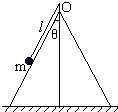
一个光滑的圆锥体固定在水平桌面上，其轴线沿竖直方向，母线与轴线之间的夹角
如图所示，一个光滑的圆锥体固定在水平桌面上，其轴线沿竖直方向，母线与轴线之间的夹角为θ=30°．一长为L的轻绳一端固定在圆锥体的顶点O处，另一端拴着一个质量为m的小物体．物体以速度v绕圆锥体的轴线在水平面内做匀速圆周运动．（结果可保留根式）
如图所示，一个光滑的圆锥体固定在水平圆盘上，其轴线沿竖直方向并与圆盘中心重合，母线与轴线间的夹角为θ．一条长为l的细绳，一端固定在圆锥体的顶点O处，另一端拴着一质量为m的小球（可视为质点）．现让圆锥体绕其中心轴线由静止开始转动，求当其角速度由零增大到
如图所示，一个光滑的圆锥体固定在水平桌面上，其轴线沿竖直方向，母线与轴线的夹角θ=30°，一条长为l的绳，一端固定在圆锥体的顶点O，另一端系一个质量为m的小球（可视为质点），小球以角速度ω绕圆锥体的轴线在水平面内做匀速圆周运动．试分析：
时，求绳对物体的拉力；
时，求绳对物体的拉力.