题目内容
如图4-5所示,一个光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,母线与轴线之间的夹角为θ=30°.一条长为L的绳(质量不计),一端固定在圆锥体的顶点O处,另一端拴着一个质量为m的小物体(物体可看作质点),物体以速率v绕圆锥体的轴线做水平匀速圆周运动.
图4-5
(1)当v=![]() 时,求绳对物体的拉力;
时,求绳对物体的拉力;
(2)当v=![]() 时,求绳对物体的拉力.
时,求绳对物体的拉力.
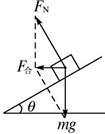
解析:水平方向:FTsinθ-FNcosθ=![]() ①
①
竖直方向:FTcosθ+FNsinθ=mg ②
联立①②两式解得:FN=mgsinθ-![]()
由上可看出当θ、L、m一定时,线速度v越大,支持力FN越小,当v满足一定条件,设v=v0时,能使FN=0,此时锥面与物体间恰好无相互作用,即mgsinθ-![]() =0
=0
v0=![]()
将θ=30°代入上式得v0=![]() .
.
(1)当v1=![]() <v0时,物体在锥面上运动,联立①②两式解得
<v0时,物体在锥面上运动,联立①②两式解得
FT1=mgcosθ+![]() =1.03mg.
=1.03mg.
(2)当v2=![]() >v0时,物体己离开锥面,但仍绕轴线做水平面内的匀速圆周运动,设此时绳与轴线间的夹角为α(α>θ),物体仅受重力和拉力作用,这时FT2sinα=
>v0时,物体己离开锥面,但仍绕轴线做水平面内的匀速圆周运动,设此时绳与轴线间的夹角为α(α>θ),物体仅受重力和拉力作用,这时FT2sinα=![]() ③
③
FT2cosα=mg ④
联立③④两式解得cosα=![]()
所以α=60°
FT2=mgcosα+![]() =
=![]() =2mg.
=2mg.
答案:(1)1.03mg (2)2mg

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目


 16、如图4—5所示,汽车质量为1.5×104 kg,以不变的速率先后驶过凹形桥面和凸形桥面,桥面圆弧半径为15 m,如果桥面承受的最大压力不得超过2.0×105 N,汽车允许的最大速率是多少?汽车以此速率驶过桥面的最小压力是多少?(g=10 m/s2)
16、如图4—5所示,汽车质量为1.5×104 kg,以不变的速率先后驶过凹形桥面和凸形桥面,桥面圆弧半径为15 m,如果桥面承受的最大压力不得超过2.0×105 N,汽车允许的最大速率是多少?汽车以此速率驶过桥面的最小压力是多少?(g=10 m/s2)