Question

如图所示，一个光滑的圆锥体固定在水平桌面上，其轴线沿竖直方向，母线与轴线的夹角θ=30°，一条长为l的绳，一端固定在圆锥体的顶点O，另一端系一个质量为m的小球（可视为质点），小球以角速度ω绕圆锥体的轴线在水平面内做匀速圆周运动．试分析：
（1）小球以角速度ω=

2g 3l

转动时，绳子的拉力和圆锥体对小球的支持力；
（2）小球以角速度ω=2

g 3l

转动时，绳子的拉力和圆锥体对小球的支持力．

Answer 1

分析：求出物体刚要离开锥面时的速度，此时支持力为零，根据牛顿第二定律求出该临界速度．当速度大于临界速度，则物体离开锥面，当速度小于临界速度，物体还受到支持力，根据牛顿第二定律，物体在竖直方向上的合力为零，水平方向上的合力提供向心力，求出绳子的拉力．

解答：解：当物体刚离开锥面时：Tcosθ-mg=0，
由拉力与重力的合力提供向心力，则有：mgtanθ=mωo2lsinθ
解之得：ω0=

2 3 g 3l

当小球以角速度₁=

2g 3l

＜ω₀时，则存在球受到斜面的支持力，因此由支持力、重力与拉力的合力提供向心力．
对球受力分析，如图所示，则有
Tsinθ-Ncosθ=m

ω

2 1

lsinθ①
Tcosθ+Nsinθ=mg②
由①②联式解之得：N=

1

2

mg-

3

6

mg，
T=

3

2

mg+

1

6

mg
当小球以角速度ω₂=2

g 3l

＞ω₀时，则球只由重力与拉力的合力提供向心力，且细绳与竖直方向夹角已增大．
如图所示，则有Tsinα=m

ω

2 2

lsinα①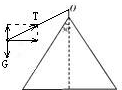
Tcosα=mg②
由①②联式解得：T=

4

3

mg
球离开斜面，则有N=O
答：（1）小球以角速度ω=

2g 3l

转动时，绳子的拉力

3

2

mg+

1

6

mg和圆锥体对小球的支持力(

1

2

-

3

6

)mg；
（2）小球以角速度ω=2

g 3l

转动时，绳子的拉力

4

3

mg和圆锥体对小球的支持力为零．

点评：解决本题的关键找出物体的临界情况，以及能够熟练运用牛顿第二定律求解．