题目内容
【题目】如图所示,质量为m=2kg的物体放在粗糙的水平地面上,与地面间的动摩擦因数μ=0.2,在大小为F=10N、方向与水平面成37°斜向下的力作用下向右做匀加速直线运动.(sin37°=0.6,cos37°=0.8,g=10m/s2)求: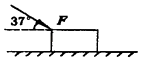
(1)物体受到的滑动摩擦力的大小Ff;
(2)5s内物体的位移的大小x.
【答案】
(1)
受力分析如图所示
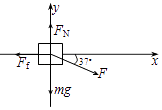
由竖直方向上物体受力平衡得:FN=mg+Fsin37°
则 Ff=μFN
联立解得 Ff=5.2N
答:物体受到的滑动摩擦力的大小Ff是5.2N.
(2)
由牛顿第二定律得Fcos37°﹣Ff=ma得 a=1.4m/s2
由位移公式 x= ![]() =
= ![]() m=17.5m
m=17.5m
答: 5s内物体的位移的大小x是17.5m.
【解析】(1)以物体为研究对象进行受力分析,由竖直方向的力平衡求出地面对物体的支持力,再求滑动摩擦力的大小Ff;(2)根据牛顿第二定律求得加速度,再位移公式求5s内物体的位移的大小x.

练习册系列答案
相关题目
【题目】某品牌电动自行车的铭牌如下;
车型:20吋 车轮直径:508 mm | 电池规格:36 V 12 Ah(安时) |
整车质量:40 kg | 额定转速:210 r/min(转/分) |
电机:后轮驱动、直流永磁式电机 | 额定工作电压/电流:36 V/5 A |
根据此铭牌中的有关数据,可知该车电机的额定功率为 W;如果以额定功率在平直公路上行驶,一次充满电最长可以行驶的时间为 h。