��Ŀ����
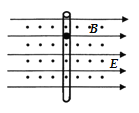
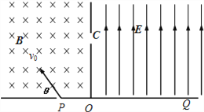
����Ŀ����ͼ��ʾ�������У����Ϊ��ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��B��Сδ֪���ұ���һ���糡ǿ�ȴ�СΪ![]() ����ǿ�糡���䷽��ƽ����OC�����Ҵ�ֱ�ڴų�������һ���ٶȴ�СΪv0������Ϊm�������Ϊ-q�Ĵ������Ӵ�P������߽���PQ�ļн���=60���ķ���������ǿ�ų���ǡ�ôӾ�O�����Ϸ�L����C�㴹ֱ��OC������ǿ�糡��������Q�㣬�������ӵ���������
����ǿ�糡���䷽��ƽ����OC�����Ҵ�ֱ�ڴų�������һ���ٶȴ�СΪv0������Ϊm�������Ϊ-q�Ĵ������Ӵ�P������߽���PQ�ļн���=60���ķ���������ǿ�ų���ǡ�ôӾ�O�����Ϸ�L����C�㴹ֱ��OC������ǿ�糡��������Q�㣬�������ӵ���������
��1���Ÿ�Ӧǿ��B�Ĵ�С��
��2�������Ӵ�P��Q����ʱ�估OQ�ij��ȣ�
��3��������ֵ糡��ų����䣬�����������ҶԵ����ҴŸ�Ӧǿ�ȴ�С��Ϊԭ����1/4���糡ǿ�ȼ�С��ԭ����һ�룬�����Դ�P�����ٶ�v0��ijһ�������룬ǡ�ô�O�����Ϸ���С��C������ǿ�ų��������ӽ���ų�����Բ���˶��İ뾶�Ƕ��٣�
���𰸡���1��![]() ��2��
��2��![]() 2L�� ��3��
2L�� ��3��![]()
��������
��1�����������ڴų���������Բ���˶��Ĺ켣���ɼ��ι�ϵ��֪��r+rcos600=L
�����������ṩ�������ɵã�![]()
���![]()

��2�������ڴų����˶�������![]() �����ڴų����˶���ʱ��Ϊ��
�����ڴų����˶���ʱ��Ϊ�� ![]()
�����ڵ糡������ƽ���˶����ڴ�ֱ�糡����x=v0t2
��ƽ�е糡����qE=ma
![]()
������Ӵ�P�˶���Q�����õ�ʱ�䣺![]()
OQ�ij�����x=2L
��3���糡�ʹų����ҶԵ��������ڵ糡�У�![]()
�ɶ��ܶ����ɵã�![]()
�����ڴų��У�![]()
����ţ�ٵڶ����ɣ�![]()
������ӽ���ų�����Բ�������İ뾶Ϊ��![]()

 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�����Ŀ��һλͬѧ����̽��������С�뵯���쳤��֮��Ĺ�ϵ��ʵ������ļ����������±���������ݱ����������÷�����
������F/N�� | 0.50 | 1.00 | 1.50 | 2.00 |
����ԭ�����ȣ�L0/cm�� | 15.00 | 15.00 | 15.00 | 15.00 |
���ɺ������ȣ�L/cm�� | 16.00 | 17.10 | 17.90 | 19.00 |
�����쳤����x/cm�� |
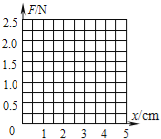
��1�����ÿһ�ε��ɵ��쳤����������������ϱ��Ŀո��ڣ�
��2��������ͼ������F��xͼ�ߣ�
��3��д��ͼ�ߵĺ�������ʽ��F��N����λ��x��m����λ���� ��
��4����ͬѧͨ������ʵ��̽���Ľ���Ӧ���ǣ� ��