题目内容
【题目】如图所示，足够长的光滑U形导轨宽度为L，其所在平面与水平面的夹角为α，上端连接一个阻值为R的电阻．匀强磁场的磁感应强度大小为B，方向垂直于导轨平面向上．今有一质量为m、有效电阻r的金属杆沿框架由静止下滑，设磁场区域无限大，当金属杆下滑达到最大速度vm时，运动的位移为x，求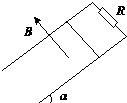
（1）金属杆沿斜面下滑的最大速度？
（2）在此过程中电阻R产生的焦耳热为多少？
（3）在此过程中流过电阻R的电荷量q为多少？
【答案】
（1）
解：金属杆下滑达到最大速度vm时做匀速直线运动，则有：mgsinα= 
，
得：vm= 
．
答：金属杆沿斜面下滑的最大速度为 ；
（2）
解：根据能量守恒定律得：在此过程中回路中产生的总热量为：Q=mgxsinα﹣ 
mvm2，
电阻R产生的焦耳热为：QR= 
Q= （mgxsinα﹣ mvm2）
答：在此过程中电阻R产生的焦耳热为 （mgxsinα﹣ mvm2）；
（3）
解：在此过程中流过电阻R的电荷量为：q=It= 
= 
答：在此过程中流过电阻R的电荷量q为 
．
【解析】（1）金属杆下滑达到最大速度v0时做匀速直线运动，根据安培力与速度的关系式和平衡条件求解最大速度．（2）根据能量守恒定律求解焦耳热；（3）根据q= 
求解电量；该题是电磁感应定律的综合应用，涉及的公式与知识点较多．其中通过金属棒横截面的电量q= 
，R+r应是回路的总电阻．
【考点精析】本题主要考查了电磁感应与电路和电磁感应与力学的相关知识点，需要掌握用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向；画等效电路；运用全电路欧姆定律，串并联电路性质，电功率等公式联立求解；用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向；求回路中电流强度；分析研究导体受力情况（包含安培力，用左手定则确定其方向）；列动力学方程或平衡方程求解才能正确解答此题．
