题目内容
16.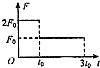 一物体在外力的作用下从静止开始做直线运动,合力F的方向不变,大小随时间的变化如图所示,设该物体在t0和3t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合力在0~t0时间内做的功是W1、在t0~3t0时间内做的功是W2,则( )
一物体在外力的作用下从静止开始做直线运动,合力F的方向不变,大小随时间的变化如图所示,设该物体在t0和3t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合力在0~t0时间内做的功是W1、在t0~3t0时间内做的功是W2,则( )| A. | x2=7x1,v2=2v1 | B. | x2=5x1,v2=$\frac{3}{2}$v1 | C. | x2=7x1,W2=3W1 | D. | v2=2v1,W2=$\frac{5}{2}$W1 |
分析 根据牛顿第二定律求出两段时间内的加速度,结合速度时间公式和位移公式求出速度的大小和位移的大小,结合功的公式求出做功的大小.
解答 解:0~t0时间内,加速度${a}_{1}=\frac{2{F}_{0}}{m}$,t0~3t0时间内,加速度${a}_{2}=\frac{{F}_{0}}{m}$,
则t0时刻的速度${v}_{1}={a}_{1}{t}_{0}=\frac{2{F}_{0}{t}_{0}}{m}$,3t0时刻的速度v2=v1+a2•2t0=$\frac{4{F}_{0}{t}_{0}}{m}$,可知v2=2v1.
t0时刻的位移${x}_{1}=\frac{1}{2}{a}_{1}{{t}_{0}}^{2}=\frac{1}{2}×\frac{2{F}_{0}}{m}{{t}_{0}}^{2}$=$\frac{{F}_{0}{{t}_{0}}^{2}}{m}$,3t0时刻的位移${x}_{2}={v}_{1}•2{t}_{0}+\frac{1}{2}{a}_{2}(2{t}_{0})^{2}$+x1=$\frac{7{F}_{0}{{t}_{0}}^{2}}{m}$,可知x2=7x1.
0~t0时间内做的功W1=2F0x1,在t0~3t0时间内做的功W2=F0(x2-x1),解得W2=3W1.故A、C正确,B、D错误.
故选:AC.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,对于求解功的关系时,也可以根据动能定理分析求解.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
6. 图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命.图乙是“轨道康复者”在某次拯救一颗地球同步卫星前,二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图,此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力,则下列说法正确的是( )
图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命.图乙是“轨道康复者”在某次拯救一颗地球同步卫星前,二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图,此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力,则下列说法正确的是( )
 图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命.图乙是“轨道康复者”在某次拯救一颗地球同步卫星前,二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图,此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力,则下列说法正确的是( )
图甲所示的“轨道康复者”航天器可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命.图乙是“轨道康复者”在某次拯救一颗地球同步卫星前,二者在同一平面内沿相同绕行方向绕地球做匀速圆周运动的示意图,此时二者的连线通过地心、轨道半径之比为1:4.若不考虑卫星与“轨道康复者”之间的引力,则下列说法正确的是( )| A. | 在图示轨道上,“轨道康复者”的速度小于7.9km/s | |
| B. | 在图示轨道上,“轨道康复者”的加速度大小是地球同步卫星的4倍 | |
| C. | 在图示轨道上,“轨道康复者”的周期为3h,且从图示位置开始经1.5h与同步卫星的距离最近 | |
| D. | 若要对该同步卫星实施拯救,“轨道康复者”应从图示轨道上加速,然后与同步卫星对接 |
7.我国自2007年开始建设“北斗二号”卫星导航系统,截止2011年4月,已陆续发射了八颗卫星,其中代号为北斗M1的卫星进入高度为21500km的运行轨道,其余七颗则进入高为36000Km的地球同步轨道,关于这些卫星,下列说法正确的是( )
| A. | 七颗同步卫星受到地球的引力一定相同 | |
| B. | “北斗二号”卫星运行速度大于7.9km/s | |
| C. | 同步卫星的向心加速度与静止在赤道上的物体的向心加速度大小相同 | |
| D. | 北斗M1绕地球运行的向心加速度比七颗同步卫星绕地球运行的向心加速度大 |
11. 质量为0.3kg的物体在水平面上运动,图中的两条直线分别表示物体受水平拉力和不受水平拉力的速度-时间图象,则下列说法中正确的是( )
质量为0.3kg的物体在水平面上运动,图中的两条直线分别表示物体受水平拉力和不受水平拉力的速度-时间图象,则下列说法中正确的是( )
 质量为0.3kg的物体在水平面上运动,图中的两条直线分别表示物体受水平拉力和不受水平拉力的速度-时间图象,则下列说法中正确的是( )
质量为0.3kg的物体在水平面上运动,图中的两条直线分别表示物体受水平拉力和不受水平拉力的速度-时间图象,则下列说法中正确的是( )| A. | 摩擦力大小一定等于0.2N | |
| B. | 水平拉力大小一定等于0.1N | |
| C. | 物体受水平拉力时的速度图象一定是b | |
| D. | 物体不受水平拉力时的速度图象一定是b |
1. 一定质量的理想气体经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与T轴平行,da与bc平行,则气体体积( )
一定质量的理想气体经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与T轴平行,da与bc平行,则气体体积( )
 一定质量的理想气体经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与T轴平行,da与bc平行,则气体体积( )
一定质量的理想气体经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与T轴平行,da与bc平行,则气体体积( )| A. | 在ab过程中不断增大 | B. | 在bc过程中保持不变 | ||
| C. | 在cd过程中不断增大 | D. | 在da过程中保持不变 |
8.关于电磁波及其应用下列说法正确的是 ( )
| A. | 麦克斯韦首先通过实验证实了电磁波的存在 | |
| B. | 电磁波是横波且能够发生干涉和衍射现象 | |
| C. | 电磁波的接收要经过调谐和调制两个过程 | |
| D. | 微波能使食物中的水分子热运动加剧从而实现加热的目的 | |
| E. | 红外线是一种光波,在军事、医疗、勘测,甚至日常生活中都有广泛的应用 |
5.下列属于核聚变反应方程的是( )
| A. | ${\;}_{7}^{15}$N+${\;}_{1}^{1}$H→${\;}_{6}^{12}$C+${\;}_{2}^{4}$He | |
| B. | ${\;}_{2}^{4}$He+${\;}_{13}^{27}$Al→${\;}_{15}^{30}$P+${\;}_{0}^{1}$n | |
| C. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He | |
| D. | ${\;}_{1}^{1}$H+${\;}_{1}^{2}$H→${\;}_{2}^{3}$He+γ |
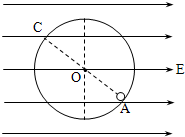 如图所示,一半径为R的光滑绝缘圆形轨道竖直放置,一质量为m,电荷量为q的小球(可视为近质点)可以在轨道内则运动.当在轨道所在的区域内加上水平向右的匀强电场时,小球可静止在图中的A点,OA与竖直方向的夹角为53°.图中C点与A点在同一直径上.求:
如图所示,一半径为R的光滑绝缘圆形轨道竖直放置,一质量为m,电荷量为q的小球(可视为近质点)可以在轨道内则运动.当在轨道所在的区域内加上水平向右的匀强电场时,小球可静止在图中的A点,OA与竖直方向的夹角为53°.图中C点与A点在同一直径上.求: 2013年6月20日,我国第一位“太空教师”王亚平举行的太空授课,其中一个内容是太空质量的测量.实验过程是聂海胜把自己固定在“质量测量仪”支架一端,王亚平拉开支架,一放手,支架在弹簧的作用下回复原位.LED屏显示出聂海胜的质量.
2013年6月20日,我国第一位“太空教师”王亚平举行的太空授课,其中一个内容是太空质量的测量.实验过程是聂海胜把自己固定在“质量测量仪”支架一端,王亚平拉开支架,一放手,支架在弹簧的作用下回复原位.LED屏显示出聂海胜的质量.