题目内容
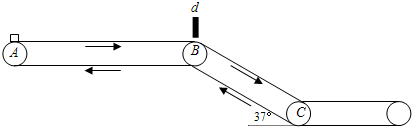
如图为一传送带装置模型,斜面的倾角θ,底端经一长度可忽略的光滑圆弧与足够长的水平传送带相连接,质量m=2kg的物体从高h=30cm的斜面上由静止开始下滑,它与斜面的动摩擦因数μ1=0.25,与水平传送带的动摩擦因数μ2=0.5,物体在传送带上运动一段时间以后,物体又回到了斜面上,如此反复多次后最终停在斜面底端.已知传送带的速度恒为v=2.5m/s,tanθ=0.75,g取10m/s2.求:
(1)从物体开始下滑到第一次回到斜面的过程中,物体与传送带因摩擦产生的热量;
(2)从物体开始下滑到最终停在斜面底端,物体在斜面上通过的总路程.

(1)从物体开始下滑到第一次回到斜面的过程中,物体与传送带因摩擦产生的热量;
(2)从物体开始下滑到最终停在斜面底端,物体在斜面上通过的总路程.

对物体从静止开始到达底端的过程运用动能定理得:
mgh-μ1mgs1cosθ=
mv12-0
代入数据解得:v1=2m/s,
物体滑上传送带后向右做匀减速运动,匀减速运动的位移为:
x1=
=
=0.4m,
匀减速运动的时间为:t1=
=
s=0.4s,
该段时间内的传送带的位移为:x2=vt1=2.5×0.4m=1m
则相对路程的大小为:△x1=x1+x2=1.4m,
返回的过程做匀加速直线运动,根据x1=
at22,
解得:t2=
=
=0.4s,
传送带的位移为:x3=vt2=2.5×0.4=1m,
则相对位移大小为:△x2=x3-x1=0.6m
相对总路程的大小为:△x=△x1+△x2=2m,
则由摩擦产生的热量为:Q=μ2mg△x=0.5×20×2J=20J.
(2)在传送带上摩擦力先做负功,再做正功,在传送带上摩擦力做功为零,对全过程运用动能定理得:
mgh-μ1mgscosθ=0
代入数据解得:s=1.5m.
答:(1)物体与传送带因摩擦产生的热量为20J;
(2)物体在斜面上通过的总路程为1.5m.
mgh-μ1mgs1cosθ=
| 1 |
| 2 |
代入数据解得:v1=2m/s,
物体滑上传送带后向右做匀减速运动,匀减速运动的位移为:
x1=
| v12 |
| 2μ2g |
| 4 |
| 10 |
匀减速运动的时间为:t1=
| v1 |
| μ2g |
| 2 |
| 5 |
该段时间内的传送带的位移为:x2=vt1=2.5×0.4m=1m
则相对路程的大小为:△x1=x1+x2=1.4m,
返回的过程做匀加速直线运动,根据x1=
| 1 |
| 2 |
解得:t2=
|
|
传送带的位移为:x3=vt2=2.5×0.4=1m,
则相对位移大小为:△x2=x3-x1=0.6m
相对总路程的大小为:△x=△x1+△x2=2m,
则由摩擦产生的热量为:Q=μ2mg△x=0.5×20×2J=20J.
(2)在传送带上摩擦力先做负功,再做正功,在传送带上摩擦力做功为零,对全过程运用动能定理得:
mgh-μ1mgscosθ=0
代入数据解得:s=1.5m.
答:(1)物体与传送带因摩擦产生的热量为20J;
(2)物体在斜面上通过的总路程为1.5m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目