题目内容
10.三个电量相同的正电荷Q,放在等边三角形的三个顶点上,问在三角形的中心应放置多大的电荷,才能使作用于每个电荷上的合力为零?分析 根据几何关系解出中心O点到三角形顶点的距离,每一个带电小球都处于静止状态,不妨研究A球,A球受力平衡,BC两球的对A是库仑斥力,O点的电荷2对A是库仑引力,列方程化简即可.
解答 解:三个电量相同的正电荷Q,放在等边三角形ABC的三个顶点上,O点为三角形中心,
设三角形边长为L,
由几何关系知:r=|AO|=$\frac{\frac{L}{2}}{cos30°}$=$\frac{\sqrt{3}}{3}$L,
A球受力平衡,有:
F2=$\frac{kQq}{{r}^{2}}$=F1=2Fcos 30°
其中F=$\frac{k{Q}^{2}}{{L}^{2}}$,
所以q=$\frac{{\sqrt{3}}}{3}Q$,由F2的方向知q带负电.
答:在三角形的中心应放置$\frac{{\sqrt{3}}}{3}Q$的负电荷,才能使作用于每个电荷上的合力为零.
点评 本题关键是要能正确的选择研究对象,由于三个小球均处于静止状态,以其中一个球为研究对象根据平衡条件得出中心O点的电荷量,根据受力方向判断电荷的正负.

练习册系列答案
相关题目
20.在圆轨道上运动的质量为m的人造地球卫星,它到地面的距离等于地球半径R,地面上的重力加速度为g,则( )
| A. | 卫星运动的加速度为$\frac{1}{2}$g | B. | 卫星运动的周期为4π$\sqrt{\frac{2R}{g}}$ | ||
| C. | 卫星运动的速度为$\sqrt{2Rg}$ | D. | 卫星运动的速度大小为$\sqrt{\frac{1}{2}gR}$ |
15.一人站在某车的一端,车原来相对于光滑地面静止,则( )
| A. | 人在车上往返行走时,车的运动方向保持不变 | |
| B. | 人从车的一端走向另一端的过程中,车向相反方向运动 | |
| C. | 人在车上走动时,若人相对车突然静止,则车因惯性沿人运动的相反方向作匀速运动 | |
| D. | 人在车上走动时,若人相对车突然静止,则车也同时停止运动 |
19.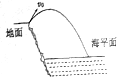 如图,在地面上以速度v0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,若以地面为零势能参考面,且不计空气阻力,则( )
如图,在地面上以速度v0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,若以地面为零势能参考面,且不计空气阻力,则( )
 如图,在地面上以速度v0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,若以地面为零势能参考面,且不计空气阻力,则( )
如图,在地面上以速度v0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,若以地面为零势能参考面,且不计空气阻力,则( )| A. | 重力对物体做的功为mgh | |
| B. | 物体在海平面的重力势能为mgh | |
| C. | 物体在海平面上的动能为 $\frac{1}{2}$mv02+mgh | |
| D. | 物体在海平面上的机械能为 $\frac{1}{2}$mv02+mgh |
 如图所示,有一块木板静止在足够长的粗糙水平面上,木板质量为M=4kg,长为L=1.4m,木板右端放着一小滑块,小滑块质量为m=1kg,可视为质点,小滑块与木板之间的动摩擦因数为μ1=0.4,木板与地面之间的动摩擦因数为μ2=0.1,取g=10m/s2.
如图所示,有一块木板静止在足够长的粗糙水平面上,木板质量为M=4kg,长为L=1.4m,木板右端放着一小滑块,小滑块质量为m=1kg,可视为质点,小滑块与木板之间的动摩擦因数为μ1=0.4,木板与地面之间的动摩擦因数为μ2=0.1,取g=10m/s2. 为了探究弹簧弹力F和弹簧伸长量x的关系,某同学选了A、B两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线的原因是超出弹性限度.弹簧A的劲度系数为$\frac{100}{3}$(可用分数表示).若要制作一个精确度较高的弹簧秤,应选弹簧A(填“A”或“B”).
为了探究弹簧弹力F和弹簧伸长量x的关系,某同学选了A、B两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线的原因是超出弹性限度.弹簧A的劲度系数为$\frac{100}{3}$(可用分数表示).若要制作一个精确度较高的弹簧秤,应选弹簧A(填“A”或“B”).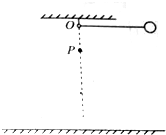 如图所示,质量为m的小球用长为l且不可伸长的细线拴住且悬于O点,悬点O距离地面高为2l,细线所受拉力达到F=9mg时就会被拉断.在悬点正下方P点固定一枚钉子,现将小球拉至与悬点O等高,并使细绳伸直,然后由静止释放,摆到悬点的正下方时细线碰到钉子.(小球半径忽略不计,不考虑阻力及线与钉子碰撞时的能量损失)
如图所示,质量为m的小球用长为l且不可伸长的细线拴住且悬于O点,悬点O距离地面高为2l,细线所受拉力达到F=9mg时就会被拉断.在悬点正下方P点固定一枚钉子,现将小球拉至与悬点O等高,并使细绳伸直,然后由静止释放,摆到悬点的正下方时细线碰到钉子.(小球半径忽略不计,不考虑阻力及线与钉子碰撞时的能量损失)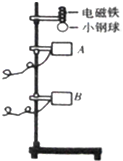 某同学用如图所示的实验装置验证机械能守恒定律,将电磁铁断电后,小钢球由静止开始自由下落,测得小钢球通过光电门A所用的时间为t1,通过光电门B所用的时间为t2,为了验证小钢球通过A、B时的机械能是否相等,除了已经测得小钢球的直径d外,还需要进行一些必要的测量、分析和判断.(已知当地重力加速度为g)
某同学用如图所示的实验装置验证机械能守恒定律,将电磁铁断电后,小钢球由静止开始自由下落,测得小钢球通过光电门A所用的时间为t1,通过光电门B所用的时间为t2,为了验证小钢球通过A、B时的机械能是否相等,除了已经测得小钢球的直径d外,还需要进行一些必要的测量、分析和判断.(已知当地重力加速度为g)