题目内容
20.在圆轨道上运动的质量为m的人造地球卫星,它到地面的距离等于地球半径R,地面上的重力加速度为g,则( )| A. | 卫星运动的加速度为$\frac{1}{2}$g | B. | 卫星运动的周期为4π$\sqrt{\frac{2R}{g}}$ | ||
| C. | 卫星运动的速度为$\sqrt{2Rg}$ | D. | 卫星运动的速度大小为$\sqrt{\frac{1}{2}gR}$ |
分析 根据万有引力等于重力,求出地球表面重力加速度与地球质量的关系.卫星绕地球做匀速圆周运动,由地球的万有引力充当向心力,列式卫星运动的速度、周期、加速度、动能与轨道半径的关系
解答 解:A、人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设地球质量为M、卫星的轨道半径为r
则 $\frac{GMm}{(2R)^{2}}=m\frac{{v}^{2}}{2R}$…①
忽略地球自转的影响有
$\frac{GMm}{{R}^{2}}=mg$…②
①②联立得:v=$\sqrt{\frac{1}{2}gR}$,
根据牛顿第二定律得:
$\frac{GMm}{{(2R)}^{2}}=ma$
解得:a=$\frac{1}{4}$g,故AC错误,D正确;
B、根据圆周运动知识得:
卫星运动的周期T=$\frac{2π•2R}{v}=4π\sqrt{\frac{2R}{g}}$,故B正确;
故选:BD
点评 解决本题的关键掌握万有引力等于重力及万有引力等于向心力,知道重力加速度与距离中心天体球心距离的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 滑板运动是非常受欢迎的运动,如图所示为滑板运动训练轨道简化图,装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接(图中未画出),轨道与滑板间的动摩擦因数都相同,为方便训练AB轨道可以适当调整,CD轨道固定.若运动员从A静止开始下滑则刚好能到达D,那么将AB轨道向右平移后从A正上方A1静止滑下,则( )
滑板运动是非常受欢迎的运动,如图所示为滑板运动训练轨道简化图,装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接(图中未画出),轨道与滑板间的动摩擦因数都相同,为方便训练AB轨道可以适当调整,CD轨道固定.若运动员从A静止开始下滑则刚好能到达D,那么将AB轨道向右平移后从A正上方A1静止滑下,则( )
 滑板运动是非常受欢迎的运动,如图所示为滑板运动训练轨道简化图,装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接(图中未画出),轨道与滑板间的动摩擦因数都相同,为方便训练AB轨道可以适当调整,CD轨道固定.若运动员从A静止开始下滑则刚好能到达D,那么将AB轨道向右平移后从A正上方A1静止滑下,则( )
滑板运动是非常受欢迎的运动,如图所示为滑板运动训练轨道简化图,装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接(图中未画出),轨道与滑板间的动摩擦因数都相同,为方便训练AB轨道可以适当调整,CD轨道固定.若运动员从A静止开始下滑则刚好能到达D,那么将AB轨道向右平移后从A正上方A1静止滑下,则( )| A. | 不能到达D | |
| B. | 刚好能到达D | |
| C. | 若能经过D刚好到达D1,一定有AD∥A1D1 | |
| D. | 若能经过D刚好到达D1,但不一定有AD∥A1D1 |
15.在狭义相对论中,下列说法中哪些是正确的?( )
(1)一切运动物体相对于观察者的速度都不能大于真空中的光速.
(2)质量、长度、时间的测量结果都是随物体与观察者的相对运动状态而改变的.
(3)在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的.
(4)惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些.
(1)一切运动物体相对于观察者的速度都不能大于真空中的光速.
(2)质量、长度、时间的测量结果都是随物体与观察者的相对运动状态而改变的.
(3)在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的.
(4)惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些.
| A. | (1)(3)(4) | B. | (1)(2)(4) | C. | (1)(2)(3) | D. | (2)(3)(4) |
5.甲,乙两物体温度相同说明两物体的( )
| A. | 每个分子的动能-定相间 | B. | 分子的平均速率一定相同 | ||
| C. | 分子平均动能-定相同 | D. | 内能-定相同 |
12.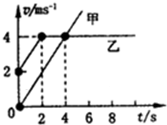 汽车甲和乙从同一地点开始向同一方向做直线运动,它们的速度--时间图象如图所示,则( )
汽车甲和乙从同一地点开始向同一方向做直线运动,它们的速度--时间图象如图所示,则( )
 汽车甲和乙从同一地点开始向同一方向做直线运动,它们的速度--时间图象如图所示,则( )
汽车甲和乙从同一地点开始向同一方向做直线运动,它们的速度--时间图象如图所示,则( )| A. | 在0-4s内,甲、乙均做匀变速直线运动 | |
| B. | 4s末乙在甲前方6m处 | |
| C. | 在0-4s内,甲的加速度大于乙的加速度 | |
| D. | 在0-4s内,乙的平均速度为3m/s |
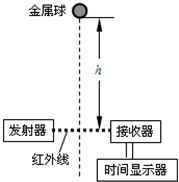 在“验证机械能守恒定律“的实验中,小明同学利用传感器设计实验:如图所示,将质量为m、直径为d的金属小球在一定高度h由静止释放,小球正下方固定一台红外线计时器,能自动记录小球挡住红外线的时间t,改变小球下落高度h,进行多次重复实验.
在“验证机械能守恒定律“的实验中,小明同学利用传感器设计实验:如图所示,将质量为m、直径为d的金属小球在一定高度h由静止释放,小球正下方固定一台红外线计时器,能自动记录小球挡住红外线的时间t,改变小球下落高度h,进行多次重复实验.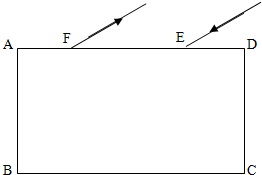 如图所示为长方形玻璃砖的截面示意图,左侧面AB和底面BC都是镀银反射面,已知边长AB=2a,AD=4a,现有一单色光从表面距D点为a的E点入射,经底面和左侧面反射后恰好从上表面的F点射出,光线在BC面和AB面上的反射点分别为M、N(图中未标出),测得AF的距离以及E点到出射光线的距离都为a,不考虑光线在AD面上的反射,则
如图所示为长方形玻璃砖的截面示意图,左侧面AB和底面BC都是镀银反射面,已知边长AB=2a,AD=4a,现有一单色光从表面距D点为a的E点入射,经底面和左侧面反射后恰好从上表面的F点射出,光线在BC面和AB面上的反射点分别为M、N(图中未标出),测得AF的距离以及E点到出射光线的距离都为a,不考虑光线在AD面上的反射,则 如图甲所示,表面绝缘、倾角θ=30°的斜面固定在水平地面上,斜面的顶端固定有弹性挡板,挡板垂直于斜面,并与斜面底边平行.斜面所在空间有一宽度D=0.40m的匀强磁场区域,其边界与斜面底边平行,磁场方向垂直斜面向上,磁场上边界到挡板的跑离s=0.55m.一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形闭合金属框abcd,放在斜面的底端,其屮ab边与斜面底边重合,ab边长L=0.50m,bc宽度与磁场宽度相等.从t=0时刻开始.线框在垂直cd边沿斜面向上大小恒定的拉力F作用下,从静止开始运动,当线框的ab边离开磁场区域时撤去拉力F,线框继续向上运动,并与挡板发生碰撞,碰撞过程的时间可忽略不计,且碰撞前后速度大小相等,方向相反.线框向上运动过程中速度与时间的v-t关系图象如图乙所示.已知线框在整个运动过程中始终未脱离斜面,且保持ab边与斜面底边平行,线框与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$.重力加速度g取10m/s2o
如图甲所示,表面绝缘、倾角θ=30°的斜面固定在水平地面上,斜面的顶端固定有弹性挡板,挡板垂直于斜面,并与斜面底边平行.斜面所在空间有一宽度D=0.40m的匀强磁场区域,其边界与斜面底边平行,磁场方向垂直斜面向上,磁场上边界到挡板的跑离s=0.55m.一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形闭合金属框abcd,放在斜面的底端,其屮ab边与斜面底边重合,ab边长L=0.50m,bc宽度与磁场宽度相等.从t=0时刻开始.线框在垂直cd边沿斜面向上大小恒定的拉力F作用下,从静止开始运动,当线框的ab边离开磁场区域时撤去拉力F,线框继续向上运动,并与挡板发生碰撞,碰撞过程的时间可忽略不计,且碰撞前后速度大小相等,方向相反.线框向上运动过程中速度与时间的v-t关系图象如图乙所示.已知线框在整个运动过程中始终未脱离斜面,且保持ab边与斜面底边平行,线框与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$.重力加速度g取10m/s2o