题目内容
以初速度v0竖直上抛一物体,已知t1末上升到h高处,在t2末又回到同一高度h处.已知重力加速度为g.试求出h 的表达式.(用v0、t1、t2、g表示)
分析:将竖直上抛运动看成一种匀减速直线运动,取竖直向上方向为正方向,加速度为-g,根据位移公式x=v0t+
at2列式求出t1、t2,再由t1?t2(t1+t2),求出h.
| 1 |
| 2 |
解答:解:取竖直向上方向为正方向,将竖直上抛运动看成一种匀减速直线运动,则加速度a=-g
由x=v0t+
at2得 h=v0t-
gt2
可解得t=
,
根据题意可得:t1=
,t2=
因此,t1?t2(t1+t2)=
,所以,h=
t1?t2(t1+t2)
答:h的表达式为h=
t1?t2(t1+t2).
由x=v0t+
| 1 |
| 2 |
| 1 |
| 2 |
可解得t=
v0±
| ||||
| g |
根据题意可得:t1=
v0+
| ||||
| g |
v0-
| ||||
| g |
因此,t1?t2(t1+t2)=
| 4v0h |
| g2 |
| g2 |
| 4v0 |
答:h的表达式为h=
| g2 |
| 4v0 |
点评:本题关键要掌握竖直上抛运动整体处理的方法,掌握其位移公式,即可求得同一高度对应的两个时间.

练习册系列答案
相关题目
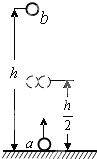 如图所示,将小球a从地面以初速度v0竖直上抛的同时,将另一相同质量的小球b从距地面h处由静止释放,两球恰在
如图所示,将小球a从地面以初速度v0竖直上抛的同时,将另一相同质量的小球b从距地面h处由静止释放,两球恰在| h |
| 2 |
| A、两球同时落地 |
| B、相遇时两球速度大小相等 |
| C、从开始运动到相遇,两球的速度变化量大小相等,方向相同 |
| D、b球刚落地时,a球恰好到达最高点 |
 从地面上以初速度v0竖直上抛一质量为m的小球,若运动过程中受到的空气阻力与其速率成正比,球运动的速率随时间变化的规律如图所示,t1时刻到达最高点,再落回地面,落地速率为v1,且落地前小球已经做匀速运动,则下列说法中错误的是( )
从地面上以初速度v0竖直上抛一质量为m的小球,若运动过程中受到的空气阻力与其速率成正比,球运动的速率随时间变化的规律如图所示,t1时刻到达最高点,再落回地面,落地速率为v1,且落地前小球已经做匀速运动,则下列说法中错误的是( )