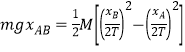��Ŀ����
����Ŀ����ͼ��ʾ����ֱ���õ�U�ι���˷�գ��Ҷ˿��ڣ���ܺ�����Ϊ�ҹܺ�������2�������������ˮ�����һ�γ�Ϊl���¶�ΪT1�Ŀ���������������ˮ����߶Ȳ�Ϊhcm��������ѹΪh0cmHg��
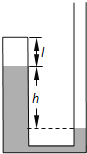
�������ҹ��л���ע��ˮ����ֱ������ˮ������ƽ��ԭ�ҹ���ˮ��ûȫ������ˮƽ���֣��������ҹ���ע��ˮ�����ij���h1����cmΪ��λ����
��������ˮ������ƽ��������������¶����������ij���Ϊ��ʼʱ�ij���l�����ʱ���������¶�T����
���𰸡���![]() ����
����![]()
��������
��1���Է������Ϊ�о������Ƚ����ͨ����ԭ�������ĩ״̬��ѹǿ��Ӧ�ò�������ɿ����������ij��ȣ����ɼ��ι�ϵ���������
��2����Һ���������½��Ĺ����У�ˮ����������ֲ��䣻�������������������ѹǿ��Ȼ��Ӧ�����������״̬�������������¶ȡ�
�ٷ��������±仯����״̬��
P1��h0��h��V1��lS
ĩ״̬��
P2��h0��V2��l��S
�ɲ�������ɣ�
P1V1��P2V2��
�������Թ��У�Һ�������ĸ߶ȣ�
��h��l��l��
��������Թ��е�ˮ���������
��V����hS
����ע���Ҳ��ˮ���������
��V0=(h+��h)S2+��V=(h+3��h)S2
�������ҹ���ע��ˮ�����ij���
h1=h+3(l-l��)��
�����٢ڵã�
![]()
�ڿ������ij���Ϊ��ʼʱ�ij���lʱ�����ˮ�����½��ص�ԭ����λ�ã���ʱ�Ҳ��ˮ���ȿ�ʼʱ�����![]() �����Ա�����
�����Ա�����![]()
��������ѹǿ��
![]()
��
��![]() ��
��
������ã� ![]()

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�