题目内容
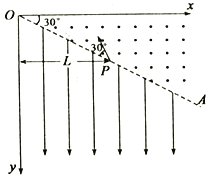
【题目】在竖直平面xoy内,分割线OA与x轴成![]() 角,分割线上方存在垂直纸面向外的匀强磁场,磁感应强度为B,下方存在电场强度为E,方向竖直向下的匀强电场和垂直纸面的匀强磁场
角,分割线上方存在垂直纸面向外的匀强磁场,磁感应强度为B,下方存在电场强度为E,方向竖直向下的匀强电场和垂直纸面的匀强磁场![]() 未画出
未画出![]() 一质量为
一质量为![]() 不计重力
不计重力![]() ,电荷量为q的带正电的粒子,从分割线OA上P点以平行纸面的速度向左上方射入磁场,粒子速度与OA成
,电荷量为q的带正电的粒子,从分割线OA上P点以平行纸面的速度向左上方射入磁场,粒子速度与OA成![]() 角,P点到y轴距离为L,带电粒子进入磁场后的运动轨迹与x轴相切,粒子从OA上另一点M射出磁场进入分割线OA下方区域时恰好做直线运动,求:
角,P点到y轴距离为L,带电粒子进入磁场后的运动轨迹与x轴相切,粒子从OA上另一点M射出磁场进入分割线OA下方区域时恰好做直线运动,求:
(1)粒子做圆周圆的速度大小;
(2)分割线下方磁场的磁感应强度大小。
【答案】(1)![]() (2)
(2)![]()
【解析】
![]() 画出粒子轨迹过程图,利用洛伦兹力提供向心力结合临界几何关系,联立即可求出粒子做圆周运动的速度大小;
画出粒子轨迹过程图,利用洛伦兹力提供向心力结合临界几何关系,联立即可求出粒子做圆周运动的速度大小;
![]() 粒子进入下方磁场时恰好做直线运动,因为洛伦兹力与速度大小有关,故粒子一定做匀速直线运动,利用受力平衡,即可求出分割线下方磁场的磁感应强度大小。
粒子进入下方磁场时恰好做直线运动,因为洛伦兹力与速度大小有关,故粒子一定做匀速直线运动,利用受力平衡,即可求出分割线下方磁场的磁感应强度大小。
![]() 画出粒子轨迹过程图如图所示,粒子在OA上方的磁场中做匀速圆周运动,
画出粒子轨迹过程图如图所示,粒子在OA上方的磁场中做匀速圆周运动,
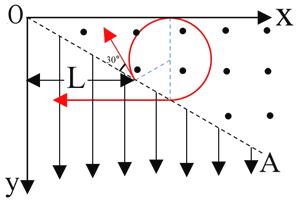
根据洛伦兹力提供向心力可得:![]()
根据几何关系可得:![]()
联立![]() 式可得粒子速度大小:
式可得粒子速度大小:![]()
![]() 设分割线下方磁场的磁感应强度大小为
设分割线下方磁场的磁感应强度大小为![]() ,粒子进入下方磁场时恰好做直线运动,分析可知一定为匀速直线运动,故粒子在分割线下方受力平衡,
,粒子进入下方磁场时恰好做直线运动,分析可知一定为匀速直线运动,故粒子在分割线下方受力平衡,
故:![]()
联立![]() 式可得:
式可得:![]()

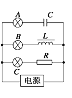
【题目】某同学通过实验制作一简易温控开关,实验原理图如图所示,当继电器电流超过10 mA时,衔铁吸合,加热器停止加热,实现温控。继电器的电阻约为20 Ω,热敏电阻与温度t的关系如下表所示。

t/℃ | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 |
R/Ω | 199.5 | 145.4 | 108.1 | 81.8 | 62.9 | 49.7 |
(1)提供的实验器材有:
电源E1(3 V,内阻不计)
电源E2(6 V,内阻不计)
滑动变阻器R1(0~20 Ω,内阻不计)
滑动变阻器R2(0~200 Ω,内阻不计)
热敏电阻Rt
电阻箱(0~999.9 Ω)
开关S,导线若干
为使该装置实验对30~80℃之间任意温度的控制,电源应选______(选填“E1”或“E2”);滑动变阻器选_______(选填“R1”或“R2”)。
(2)欲使热敏电阻为40℃时衔铁吸合,下列操作步骤正确的顺序是______。
①将热敏电阻接入电路
②观察到继电器的衔铁被吸合
③断开开关,将电阻箱从电路中移除
④合上开关,调节滑动变阻器的阻值
⑤断开开关,用变阻箱替换热敏电阻,将变阻箱电阻调至145.4 Ω
A.⑤④②③① B.③⑤④②① C.①④⑤②③ D.④⑤②③①