题目内容
(2007?淮安模拟)我国已启动“嫦娥工程”,并于2007年10月24日成功发射绕月运行的探月卫星“嫦娥Ⅰ号”.设该卫星可贴近月球表面运动且轨道是圆形的,已知地球半径约是月球半径的4倍,地球质量约是月球质量的81倍,地球近地卫星的周期约为84min,地球表面重力加速度g取10m/s2,求:
(1)绕月表面做匀速圆周运动的“嫦娥Ⅰ号”,其运动周期约是多大?
(2)设想宇航员在月球表面上做自由落体实验,某物体从离月球表面20m处自由下落,约经多长时间落地?
(1)绕月表面做匀速圆周运动的“嫦娥Ⅰ号”,其运动周期约是多大?
(2)设想宇航员在月球表面上做自由落体实验,某物体从离月球表面20m处自由下落,约经多长时间落地?
分析:1、地球近地卫星受地球的万有引力提供向心力
=m(
)2R,探月卫星它受月球的万有引力提供向心力
=m1(
)2R1,两式相比,可以求出“嫦娥Ⅰ号”的运动周期T1.
2、根据星球表面的物体受到的重力等于万有引力,在地球上有mg=G
,在月球上有m1g1=G
,两式相比,计算出月球表面重力加速度g1.再根据自由落体运动的规律h=
at12,可计算出落体运动的时间.
| GMm |
| R2 |
| 2π |
| T0 |
| GM1m1 |
| R12 |
| 2π |
| T1 |
2、根据星球表面的物体受到的重力等于万有引力,在地球上有mg=G
| Mm |
| R2 |
| M1m1 |
| R12 |
| 1 |
| 2 |
解答:解:设地球质量为M,半径为R,近地卫星的质量为m,周期为T0,它受地球的万有引力提供向心力,则
=m(
)2R
设月球质量为M1,半径为R1,探月卫星的质量为m1,周期为T1,它受月球的万有引力提供向心力,则
=m1(
)2R1
=
=
=
T1=94.5min
(2)设地球表面重力加速度g,月球表面重力加速度g1,自由下落高度为h,
根据星球表面的物体受到的重力等于万有引力,在地球和月球上都有
mg=G
m1g1=G
下式比上式得:
=
?(
)2=
×
所以g1=
m/s2
根据自由落体运动的规律
h=
at12
t1=
=
s=4.5s
答:(1)绕月表面做匀速圆周运动的“嫦娥Ⅰ号”,其运动周期约是94.5min.
(2)设想宇航员在月球表面上做自由落体实验,某物体从离月球表面20m处自由下落,约经4.5s落地.
| GMm |
| R2 |
| 2π |
| T0 |
设月球质量为M1,半径为R1,探月卫星的质量为m1,周期为T1,它受月球的万有引力提供向心力,则
| GM1m1 |
| R12 |
| 2π |
| T1 |
| T1 |
| T0 |
|
|
| 9 |
| 8 |
T1=94.5min
(2)设地球表面重力加速度g,月球表面重力加速度g1,自由下落高度为h,
根据星球表面的物体受到的重力等于万有引力,在地球和月球上都有
mg=G
| Mm |
| R2 |
m1g1=G
| M1m1 |
| R12 |
下式比上式得:
| g1 |
| g |
| M1 |
| M |
| R |
| R1 |
| 1 |
| 81 |
| 16 |
| 1 |
所以g1=
| 160 |
| 81 |
根据自由落体运动的规律
h=
| 1 |
| 2 |
t1=
|
|
答:(1)绕月表面做匀速圆周运动的“嫦娥Ⅰ号”,其运动周期约是94.5min.
(2)设想宇航员在月球表面上做自由落体实验,某物体从离月球表面20m处自由下落,约经4.5s落地.
点评:本题要求掌握天体运动中两个重要的关系;①环绕天体绕中心天体做匀速圆周运动所需要的向心力由万有引力提供,②星球表面的物体受到的重力等于万有引力.同时还要知道自由落体运动的规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
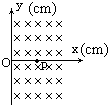 (2007?淮安模拟)如图所示在真空中XOY平面的X>0区域内,磁感应强度B=1.0×10-2T的匀强磁场,方向与XOY平面垂直,在X轴上P(10,0)点,有一放射源,在XOY平面内各个方向发射速度V=1.0×105m/S的带正电的粒子粒子质量m=1.0×10-26Kg粒子的带电量为q=1.0×10-18C,则带电粒子打到y轴上的范围为
(2007?淮安模拟)如图所示在真空中XOY平面的X>0区域内,磁感应强度B=1.0×10-2T的匀强磁场,方向与XOY平面垂直,在X轴上P(10,0)点,有一放射源,在XOY平面内各个方向发射速度V=1.0×105m/S的带正电的粒子粒子质量m=1.0×10-26Kg粒子的带电量为q=1.0×10-18C,则带电粒子打到y轴上的范围为