题目内容
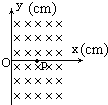（2007?淮安模拟）如图所示在真空中XOY平面的X＞0区域内，磁感应强度B=1.0×10-2T的匀强磁场，方向与XOY平面垂直，在X轴上P（10，0）点，有一放射源，在XOY平面内各个方向发射速度V=1.0×105m/S的带正电的粒子粒子质量m=1.0×10-26Kg粒子的带电量为q=1.0×10-18C，则带电粒子打到y轴上的范围为-10cm～17.32cm
-10cm～17.32cm
（重力忽略）分析：带电粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律求出粒子的轨道半径；作出粒子运动轨迹然后求出粒子打到y轴上的范围．
解答：
解：洛伦兹力提供向心力，由牛顿第二定律得：qvB=m
，
解得，粒子的轨道半径R=0.1m，
由左手定则可知，粒子在磁场中沿逆时针做圆周运动，粒子的运动轨迹过P点，
粒子离开P点的最大距离为2R，以P为圆心，2R为半径做圆，交y轴与A点，
A是粒子打在y轴上的最远点，粒子在y轴负半轴上的最远点为B，如图所示，
由几何知识得：OA=
=
=0.1
m=0.1732m=17.32cm，
OB=R=0.1m=10cm，粒子打到y轴上的范围是-10cm～17.32cm；
故答案为：-10cm～17.32cm．
解：洛伦兹力提供向心力，由牛顿第二定律得：qvB=m| v2 |
| R |
解得，粒子的轨道半径R=0.1m，
由左手定则可知，粒子在磁场中沿逆时针做圆周运动，粒子的运动轨迹过P点，
粒子离开P点的最大距离为2R，以P为圆心，2R为半径做圆，交y轴与A点，
A是粒子打在y轴上的最远点，粒子在y轴负半轴上的最远点为B，如图所示，
由几何知识得：OA=
| (2R)2-OP2 |
| (2×0.1)2-0．12 |
| 3 |
OB=R=0.1m=10cm，粒子打到y轴上的范围是-10cm～17.32cm；
故答案为：-10cm～17.32cm．
点评：本题考查了带电粒子在匀强磁场中的运动，根据题意作出粒子的运动轨迹是正确解题的前提与关键．
练习册系列答案
相关题目
