Question

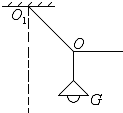（2011?河南模拟）天花板上用电线吊着一个重为G电灯，电线的自重不计，用一根能够承受

3

4

G拉力的细线系在距悬点O₁为 1.5m处的O点，沿水平方向拉动电线，使电灯偏离开悬点O₁的正下方，如图所示．
求：
（1）电灯可以偏离开悬点O₁正下方的最大水平距离是多少？
（2）此时上段电线O₁O的拉力是多少？

Answer 1

分析：（1）对点O受力分析，受电灯的拉力（大小等于重力G）、电线O₁O的拉力T，细线向右的拉力F；根据平衡条件并结合正交分解法列方程求解；
（2）根据第一问可得电线O₁O的拉力．

解答：解：（1）对点O受力分析，如图

x方向：Tsinα=F
y方向：Tcosα=mg
解得：
tanα=

F

G

=

3 4 G

G

=

3

4

（α=37°）
T=

F

sinα

=

3 4 G

3 5

=

5

4

G
所以
x=hsinα=1.5×0.6=0.9m
故电灯可以偏离开悬点O₁正下方的最大水平距离是0.9m．
（2）由第一问可得
T=

F

sinα

=

3 4 G

3 5

=

5

4

G
故绳子即将断开时，上段电线O₁O的拉力是

5

4

G．

点评：本题关键是对点O受力分析，然后根据平衡条件并结合正交分解法列式求解，找出绳子即将断开的临界状态也很重要．