题目内容
(15分)甲车以10m/s的速度在平直的公路上匀速行驶,乙车以4m/s的速度与甲车平行同向做匀速直线运动,甲车经过乙车旁边开始以0.5 m/s2的加速度刹车,从甲车刹车开始计时,求:
(1)乙车在追上甲车前,两车相距的最大距离;
(2)乙车追上甲车所用的时间.
(1) 36m (2) 25s
解析试题分析:(1)当甲车速度减至等于乙车速度时两车的距离最大,设该减速过程经过的时间为t,则
v乙=v甲-at,解得:t=12s 2分
此时甲、乙间距离为
Δx=(v甲t-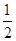 at2)-v乙t 2分
at2)-v乙t 2分
=10×12m-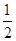 ×0.5×122m-4×12m=36m. 3分
×0.5×122m-4×12m=36m. 3分
(2)设甲车减速到零所需时间为t1,则有:
t1=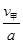 =20s. 1分
=20s. 1分
t1时间内,x甲=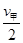 t1=
t1= ×20m=100m 1分
×20m=100m 1分
x乙=v乙t1=4×20m=80m 1分
此后乙车运动时间t2=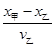 =
=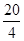 s=5s 2分
s=5s 2分
故乙车追上甲车需t1+t2=25s. 3分
考点:本题考查追击相遇问题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
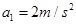 ;减速上升时,加速度大小
;减速上升时,加速度大小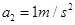
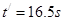 ,电梯上升的高度是多少?
,电梯上升的高度是多少? 的加速度做匀加速直线运动,求:
的加速度做匀加速直线运动,求: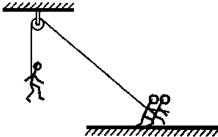

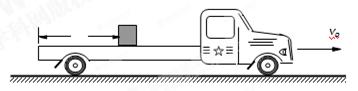
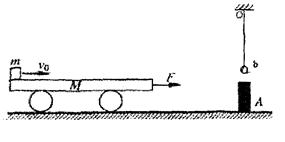
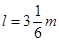 ,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做 a1 =" 3" m/s2的匀减速直线运动。已知货箱与平板车之间的摩擦因数为 μ =" 0.2" , g =" 10" m/s2。求:
,货箱放到车上的同时,平板车开始刹车,刹车过程可视为做 a1 =" 3" m/s2的匀减速直线运动。已知货箱与平板车之间的摩擦因数为 μ =" 0.2" , g =" 10" m/s2。求: