Question

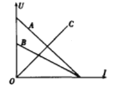
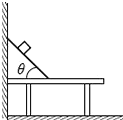
【题目】如图所示，用一块长L1=1.0m的木板在墙和桌面间架设斜面，桌面离地高H=0.8m，桌面长L2=1.5m，斜面和水平桌面间的倾角θ可以在060°之间调节后固定，将质量m=0.2kg的小物块从斜面顶端无初速释放，物块与斜面间的动摩擦因数μ1=0.05，物块和桌面间的动摩擦因数为μ2，忽略物块在斜面和桌面交接处的能量损失。（已知最大静摩擦力等于滑动摩擦力）

（1）当物块刚好能从斜面开始下滑时，求斜面的倾角θ；（用正切值表示）

（2）当θ角增大到37°时，物块下滑后恰能停在桌面边缘，求物块与桌面间的动摩擦因数μ2；

（3）若将（2）中求出的μ2作为已知条件，继续增大θ角，求物块落地点与墙面的距离最大值S总，及此时斜面的倾角θ。

Answer 1

【答案】（1）tanθ= 0.05；（2）0.8；（3）1.9m，53°。

【解析】

（1）当物块刚好能从斜面开始下滑时，有

mgsinθ=μ1mgcosθ

解得：

tanθ=μ1=0.05，

斜面的倾角

θ=arctan0.05

（2）物块从顶端无初速释放开始直至恰好停在桌面边缘，根据动能定理 W合=得：

mgL1sin37°﹣μ1mg L1cos37°﹣μ2mg（L2﹣L1cos37°）=0

代入数据，解得

μ2=0.8

（3）物块从顶端无初速释放开始直至运动到桌面末端，根据动能定理得：

mgL1sinθ﹣μ1mg L1cosθ﹣μ2 mg（L2﹣L1cosθ）=

代入数据得

sinθ+0.75 cosθ﹣1.2=

变形得

（sinθcosα+sinαcosθ）﹣1.2=

式中tanα=0.75，α=37°，即

sin（θ+37°）﹣1.2=

则当θ=53°时，有最大值，解得v的最大值为vm=1m/s。

对于平抛运动，竖直方向有：

H=gt2

代入数据，解得物块离开桌面平抛的时间t=0.4s，平抛运动的水平距离最大为

x=vmt=0.4m

物块落地点与墙面的距离最大值为

S总=L2+x=1.9m

答：（1）当物块刚好能从斜面开始下滑时，斜面的倾角正切值为tanθ=0.05；（2）当θ角增大到37°时，物块下滑后恰能停在桌面边缘，物块与桌面间的动摩擦因数μ2是0.8；（3）物块落地点与墙面的距离最大值S总是1.9m，此时斜面的倾角θ是53°。