题目内容
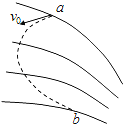
【题目】如图所示,带正电的A球固定在足够大的光滑绝缘斜面上,斜面的倾角α=37°,其带电量Q= ![]() ×10﹣5C;质量m=0.1kg、带电量q=+1×10﹣7C的B球在离A球L=0.1m处由静止释放,两球均可视为点电荷.(静电力恒量k=9×109Nm2/C2,sin37°=0.6,cos37°=0.8)
×10﹣5C;质量m=0.1kg、带电量q=+1×10﹣7C的B球在离A球L=0.1m处由静止释放,两球均可视为点电荷.(静电力恒量k=9×109Nm2/C2,sin37°=0.6,cos37°=0.8)

(1)A球在B球释放处产生的电场强度大小和方向;
(2)B球的速度最大时两球间的距离;
(3)若B球运动的最大速度为v=4m/s,求B球从开始运动到最大速度的过程中电势能怎么变?变化量是多少?
【答案】(1)2.4×107N/C,方向沿斜面向上 (2)0.2m (3)0.86J
【解析】
(1)根据点电荷场强公式E=kQ/r2 求A球在B球释放处产生的电场强度大小和方向;
(2)当静电力等于重力沿斜面向下的分力时B球的速度最大,根据库仑定律和平衡条件求两球间的距离;
(3)B球减小的电势能等于它动能和重力势能的增加量,根据功能关系求解.
(1)A球在B球释放处产生的电场强度大小![]() =2.4×107N/C;
=2.4×107N/C;
方向沿斜面向上.
(2)当静电力等于重力沿斜面向下的分力时B球的速度最大,
即:F=k![]() =mgsinα
=mgsinα
解得 r=0.2m;
(3)由于r>L,可知,两球相互远离,则B球从开始运动到最大速度的过程中电场力做正功,电势能变小;
根据功能关系可知:B球减小的电势能等于它动能和重力势能的增加量,所以B球电势能变化量为:△Ep=[![]() mv2+mg(r-L)sinα]
mv2+mg(r-L)sinα]
解得,△Ep=0.86J

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目