题目内容
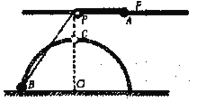
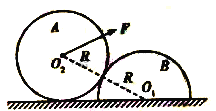
【题目】如图所示,光滑圆柱A和半圆柱B紧靠着静置于水平地面上,二者半径均为R。A的质量为m,B的质量为![]() ,B与地面的动摩擦因数为μ。现给A施加一拉力F,使A缓慢移动,运动过程中拉力F与圆心连线O1O2的夹角始终为60°保持不变,直至A恰好运动到B的最高点,整个过程中B保持静止,设最大静摩擦力等于滑动摩擦力,重力加速度为g,求:
,B与地面的动摩擦因数为μ。现给A施加一拉力F,使A缓慢移动,运动过程中拉力F与圆心连线O1O2的夹角始终为60°保持不变,直至A恰好运动到B的最高点,整个过程中B保持静止,设最大静摩擦力等于滑动摩擦力,重力加速度为g,求:
(1)A、B间弹力的最大值Fmax
(2)动摩擦因数的最小值μmin
【答案】(1) ![]() (2)
(2) ![]()
【解析】(1)以A为研究对象,受重力mg,拉力F,B对A的弹力FN;由题意,三个力的合力始终为零,矢量三角形如图,在FN转至竖直的过程中,AB间弹力先增大后减小,拉力F逐渐减小,当θ=300(F水平向右)时,AB间弹力最大, ![]()

(2)对B受力分析可知,竖直方向水平地面的支持力![]() ,可知水平地面对B的支持力逐渐增大;
,可知水平地面对B的支持力逐渐增大;
水平方向的静摩擦力f=FNsinθ可知静摩擦力逐渐减小,所以只要初状态不滑动,以后就不会滑动,即![]() ,初状态时,圆柱A对圆柱B的弹力FN=mg,带入数据可得:
,初状态时,圆柱A对圆柱B的弹力FN=mg,带入数据可得: ![]()

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目