题目内容

如图所示，光滑的直角三角形框架ABC竖直放在水平面上，两质量均为m的小环M、N用轻质细绳相连套在两直角边上而处于静止状态，已知θ=30°，则下列判断正确的是

A.
细绳张力大小为 $数学公式$ mg
B.
环M对AB边压力为mg
C.
环M、N对两直角边的压力的比值为 $数学公式$
D.
剪断细绳瞬间，环M、N的加速度之比为 $数学公式$ ：3

D
分析：对两个环分别受力分析，均受重力、支持力和拉力，根据平衡条件列式求解．
解答：A、B、C、对两个环分别受力分析，均受重力、支持力和拉力；
对M环，根据平衡条件，有：
Tcosα=mgsinθ ①
Tsinα+mgcosθ-N=0 ②
对N环，根据平衡条件，有：
Tsinα=mgcosθ ③
Tcosα+mgsinθ-N′=0 ④
联立解得：T=mg
N=N′= $\text{[math]}$ mg
α=60°
D、剪断细绳瞬间，环受重力和支持力，根据牛顿第二定律，有：
M环：mgsin30°=ma
N环：mgsin60°=ma′
故a：a′= $\text{[math]}$ ：3
故ABC错误，D正确；
故选D．
点评：本题关键分别对M和N两个环受力分析，然后根据平衡条件列方程求解未知量，不难．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

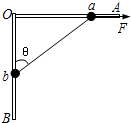如图所示，光滑的直角细杆AOB固定在竖直平面内，OA杆水平，OB杆竖直．有两个质量相等均为0.3kg的小球a与b分别穿在OA、OB杆上，两球用一轻绳连接，轻绳长L=25cm．两球在水平拉力F作用下目前处于静止状态，绳与OB杆的夹角θ=53°，求：
（1）此时细绳对小球b的拉力大小，水平拉力F的大小；
（2）现突然撤去拉力F，两球从静止开始运动，设OB杆足够长，运动过程中细绳始终绷紧，则当θ=37°时，小球b的速度大小．
（sin37°=0.6，cos37°=0.8，sin53°=0.8，cos53°=0.6）

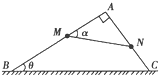如图所示，光滑的直角三角形框架ABC竖直放在水平面上，两质量均为m的小环M、N用轻质细绳相连套在两直角边上而处于静止状态，已知θ=30°，则下列判断正确的是（　　）

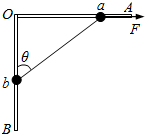如图所示，光滑的直角细杆AOB固定在竖直平面内，OA杆水平，OB杆竖直．有两个质量相等均为0.3kg的小球a与b分别穿在OA、OB杆上，两球用一轻绳连接，轻绳长L=25cm．两球在水平拉力F作用下目前处于静止状态，绳与OB杆的夹角θ=53°（sin37°=0.6，cos37°=0.8，sin53°=0.8，cos53°=0.6），求：
（1）此时细绳对小球b的拉力大小，水平拉力F的大小；
（2）现突然撤去拉力F，两球从静止开始运动，设OB杆足够长，运动过程中细绳始终绷紧，则当θ=37°时，小球b的速度大小．

如图所示，光滑的直角细杆AOB固定在竖直平面内，OA杆水平，OB杆竖直。有两个质量相等均为0.3 kg的小球a与b分别穿在OA、OB杆上，两球用一轻绳连接，轻绳长L＝25 cm。两球在水平拉力F作用下目前处于静止状态，绳与OB杆的夹角q＝53°，求：
（1）此时细绳对小球b的拉力大小，水平拉力F的大小；
（2）现突然撤去拉力F，两球从静止开始运动，设OB杆足够长，运动过程中细绳始终绷紧，则当q＝37°时，小球b的速度大小。
（sin37°＝0.6，cos37°＝0.8，sin53°＝0.8，cos53°＝0.6）

如图所示，光滑的直角细杆AOB固定在竖直平面内，OA杆水平，OB杆竖直。有两个质量相等均为0.3 kg的小球a与b分别穿在OA、OB杆上，两球用一轻绳连接，轻绳长L＝25 cm。两球在水平拉力F作用下目前处于静止状态，绳与OB杆的夹角q＝53°（sin37°＝0.6，cos37°＝0.8，sin53°＝0.8，cos53°＝0.6），求：

（1）此时细绳对小球b的拉力大小，水平拉力F的大小；

（2）现突然撤去拉力F，两球从静止开始运动，设OB杆足够长，运动过程中细绳始终绷紧，则当q＝37°时，小球b的速度大小。

如图所示，光滑的直角三角形框架ABC竖直放在水平面上，两质量均为m的小环M、N用轻质细绳相连套在两直角边上而处于静止状态，已知θ=30°，则下列判断正确的是

试题分类