题目内容
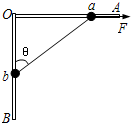 如图所示,光滑的直角细杆AOB固定在竖直平面内,OA杆水平,OB杆竖直.有两个质量相等均为0.3kg的小球a与b分别穿在OA、OB杆上,两球用一轻绳连接,轻绳长L=25cm.两球在水平拉力F作用下目前处于静止状态,绳与OB杆的夹角θ=53°,求:
如图所示,光滑的直角细杆AOB固定在竖直平面内,OA杆水平,OB杆竖直.有两个质量相等均为0.3kg的小球a与b分别穿在OA、OB杆上,两球用一轻绳连接,轻绳长L=25cm.两球在水平拉力F作用下目前处于静止状态,绳与OB杆的夹角θ=53°,求:(1)此时细绳对小球b的拉力大小,水平拉力F的大小;
(2)现突然撤去拉力F,两球从静止开始运动,设OB杆足够长,运动过程中细绳始终绷紧,则当θ=37°时,小球b的速度大小.
(sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6)
分析:(1)先对b球研究,根据共点力平衡条件救出绳子的拉力大小;再对a球研究,再次根据共点力平衡条件列式,即可求出水平拉力F的大小;
(3)撤去拉力F后,系统的机械能守恒,由机械能守恒定律列式,运用速度的分解法得到两个小球速度大小的关系,联立即可即可求得b球的速度大小.
(3)撤去拉力F后,系统的机械能守恒,由机械能守恒定律列式,运用速度的分解法得到两个小球速度大小的关系,联立即可即可求得b球的速度大小.
解答:解:先以b球为研究对象,设绳子的拉力大小为T,则由平衡条件有
Tcos53°=mg
再以a球为研究对象,则有
Tsin53°=F
联立解得,T=5N,F=mgtan53°=4N
(2)撤去拉力F后,系统的机械能守恒,则有
mg(L cos37°-L cos53°)=
mvb2+
mva2,①
又将两球的速度分解,两球沿绳子方向的分速度大小相等,则有
vbcos37°=vasin37° ②
联立①②解得,vb=0.6m/s
答:
(1)此时细绳对小球b的拉力大小为5N,水平拉力F的大小是4N.
(2)撤去拉力F,两球从静止开始运动,当θ=37°时,小球b的速度大小是0.6m/s.
Tcos53°=mg
再以a球为研究对象,则有
Tsin53°=F
联立解得,T=5N,F=mgtan53°=4N
(2)撤去拉力F后,系统的机械能守恒,则有
mg(L cos37°-L cos53°)=
| 1 |
| 2 |
| 1 |
| 2 |
又将两球的速度分解,两球沿绳子方向的分速度大小相等,则有
vbcos37°=vasin37° ②
联立①②解得,vb=0.6m/s
答:
(1)此时细绳对小球b的拉力大小为5N,水平拉力F的大小是4N.
(2)撤去拉力F,两球从静止开始运动,当θ=37°时,小球b的速度大小是0.6m/s.
点评:本题运用隔离法研究力平衡问题,也可以采用隔离法和整体法相结合的方法研究.第2问是系统机械能守恒问题,关键是寻找两球速度关系.

练习册系列答案
相关题目
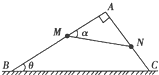 如图所示,光滑的直角三角形框架ABC竖直放在水平面上,两质量均为m的小环M、N用轻质细绳相连套在两直角边上而处于静止状态,已知θ=30°,则下列判断正确的是( )
如图所示,光滑的直角三角形框架ABC竖直放在水平面上,两质量均为m的小环M、N用轻质细绳相连套在两直角边上而处于静止状态,已知θ=30°,则下列判断正确的是( )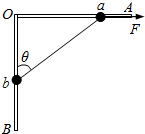 如图所示,光滑的直角细杆AOB固定在竖直平面内,OA杆水平,OB杆竖直.有两个质量相等均为0.3kg的小球a与b分别穿在OA、OB杆上,两球用一轻绳连接,轻绳长L=25cm.两球在水平拉力F作用下目前处于静止状态,绳与OB杆的夹角θ=53°(sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6),求:
如图所示,光滑的直角细杆AOB固定在竖直平面内,OA杆水平,OB杆竖直.有两个质量相等均为0.3kg的小球a与b分别穿在OA、OB杆上,两球用一轻绳连接,轻绳长L=25cm.两球在水平拉力F作用下目前处于静止状态,绳与OB杆的夹角θ=53°(sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6),求:
