题目内容
9. 如图所示,在倾角为α的斜面上,一重为G的小球被竖直的木板挡住,不计一切摩擦,则小球对木板(挡板)的压力F1和对斜面的压力F2,的大小分别是( )
如图所示,在倾角为α的斜面上,一重为G的小球被竖直的木板挡住,不计一切摩擦,则小球对木板(挡板)的压力F1和对斜面的压力F2,的大小分别是( )| A. | F1=Gsinα;F2=Gcosα | B. | F1=Gcosα;F2=Gsinα | ||
| C. | F1=Gtanα;${F_2}=\frac{G}{cosα}$ | D. | ${F_1}=\frac{G}{cosα}$;F2=Gtanα |
分析 对小球进行受力分析,此时注意小球受挡板的弹力方向,不是沿斜面向上而是垂直挡板水平向.由平衡条件求斜面和挡板对小球的弹力,再由牛顿第三定律得解.
解答 解:以小球为研究对象,建立坐标系对小球进行受力分析,运用合成法如图:
根据平衡条件和三角函数关系知:
FN1=Gtanα.
FN2=$\frac{G}{cosα}$
由牛顿第三定律得小球对木板的压力为:F1=FN1=Gtanα,对斜面的压力为:F2=FN2=$\frac{G}{cosα}$
故选:C
点评 共点力平衡问题的解题一般按如下步骤进行:1、明确研究对象.2、分析研究对象受力,作出受力示意图.3、选择合适的方法,根据平衡条件列方程求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下面有关物理学史和物理学方法的说法中,正确的有( )
| A. | 伽利略研究自由落体运动时,由于物体下落时间太短,不易测量,因此采用了“冲淡重力”的方法来测量时间,然后再把得出的结论合理外推 | |
| B. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法 | |
| C. | 由$a=\frac{△v}{△t}$可知,物体的加速度又叫做速度的变化率,所以加速度由$\frac{△v}{△t}$决定 | |
| D. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
20. 如图所示,悬挂在O点的一根不可伸长的绝缘细线下端有一个带电量不变的小球A.在两次实验中,均缓慢移动另一带同种电荷的小球B.当B到达悬点O的正下方并与A在同一水平线上,A处于受力平衡时,悬线偏离竖直方向的角度为α,若两次实验中B的电量分别为q1和q2,角度为α分别为45°和30°则$\frac{{q}_{2}}{{q}_{1}}$为( )
如图所示,悬挂在O点的一根不可伸长的绝缘细线下端有一个带电量不变的小球A.在两次实验中,均缓慢移动另一带同种电荷的小球B.当B到达悬点O的正下方并与A在同一水平线上,A处于受力平衡时,悬线偏离竖直方向的角度为α,若两次实验中B的电量分别为q1和q2,角度为α分别为45°和30°则$\frac{{q}_{2}}{{q}_{1}}$为( )
 如图所示,悬挂在O点的一根不可伸长的绝缘细线下端有一个带电量不变的小球A.在两次实验中,均缓慢移动另一带同种电荷的小球B.当B到达悬点O的正下方并与A在同一水平线上,A处于受力平衡时,悬线偏离竖直方向的角度为α,若两次实验中B的电量分别为q1和q2,角度为α分别为45°和30°则$\frac{{q}_{2}}{{q}_{1}}$为( )
如图所示,悬挂在O点的一根不可伸长的绝缘细线下端有一个带电量不变的小球A.在两次实验中,均缓慢移动另一带同种电荷的小球B.当B到达悬点O的正下方并与A在同一水平线上,A处于受力平衡时,悬线偏离竖直方向的角度为α,若两次实验中B的电量分别为q1和q2,角度为α分别为45°和30°则$\frac{{q}_{2}}{{q}_{1}}$为( )| A. | 2$\sqrt{3}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\sqrt{6}$ |
17.铁道转弯处内、外铁轨间设计有高度差,可以使火车顺利转弯,下列说法中正确的是( )


| A. | 主要是为了减少车轮与铁轨间的摩擦 | |
| B. | 主要是为了减少轮缘与铁轨间的挤压 | |
| C. | 内轨应略高于外轨 | |
| D. | 重力和支持力的合力为火车转弯提供了向心力 |
4.物体做匀加速直线运动,已知第1s初的速度的大小是6m/s,第2s末的速度大小是10m/s,则该物体的加速度不可能是( )
| A. | 2m/s2 | B. | 16 m/s2 | C. | -2 m/s2 | D. | -8 m/s2 |
1. 如图所示,某同学用细线把一块橡皮悬挂于O点,用钉子靠着线的左侧,使钉子沿与水平方向成30°角的斜面向右以速度v匀速运动,运动过程中始终保持县线竖直,下列说法正确的是( )
如图所示,某同学用细线把一块橡皮悬挂于O点,用钉子靠着线的左侧,使钉子沿与水平方向成30°角的斜面向右以速度v匀速运动,运动过程中始终保持县线竖直,下列说法正确的是( )
 如图所示,某同学用细线把一块橡皮悬挂于O点,用钉子靠着线的左侧,使钉子沿与水平方向成30°角的斜面向右以速度v匀速运动,运动过程中始终保持县线竖直,下列说法正确的是( )
如图所示,某同学用细线把一块橡皮悬挂于O点,用钉子靠着线的左侧,使钉子沿与水平方向成30°角的斜面向右以速度v匀速运动,运动过程中始终保持县线竖直,下列说法正确的是( )| A. | 橡皮的速度大小为$\sqrt{2}$v | |
| B. | 橡皮的速度大小为$\sqrt{3}$v | |
| C. | 橡皮的速度方向与水平方向成60°角 | |
| D. | 橡皮的速度方向与水平方向成45°角 |
18.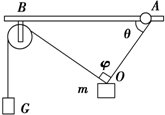 如图所示,圆环套在水平棒上可以滑动,轻绳OA的A端与圆环套(重力不计)相连,O端与质量m=1kg的重物相连;定滑轮固定在B处,跨过定滑轮的轻绳,两端分别与重物m、重物G相连,当两条细绳间的夹角φ=90°,OA与水平杆的夹角θ=53°时圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,已知sin 53°=0.8;cos 53°=0.6,滑动摩擦力等于最大静摩擦力.则下列说法正确的是( )
如图所示,圆环套在水平棒上可以滑动,轻绳OA的A端与圆环套(重力不计)相连,O端与质量m=1kg的重物相连;定滑轮固定在B处,跨过定滑轮的轻绳,两端分别与重物m、重物G相连,当两条细绳间的夹角φ=90°,OA与水平杆的夹角θ=53°时圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,已知sin 53°=0.8;cos 53°=0.6,滑动摩擦力等于最大静摩擦力.则下列说法正确的是( )
 如图所示,圆环套在水平棒上可以滑动,轻绳OA的A端与圆环套(重力不计)相连,O端与质量m=1kg的重物相连;定滑轮固定在B处,跨过定滑轮的轻绳,两端分别与重物m、重物G相连,当两条细绳间的夹角φ=90°,OA与水平杆的夹角θ=53°时圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,已知sin 53°=0.8;cos 53°=0.6,滑动摩擦力等于最大静摩擦力.则下列说法正确的是( )
如图所示,圆环套在水平棒上可以滑动,轻绳OA的A端与圆环套(重力不计)相连,O端与质量m=1kg的重物相连;定滑轮固定在B处,跨过定滑轮的轻绳,两端分别与重物m、重物G相连,当两条细绳间的夹角φ=90°,OA与水平杆的夹角θ=53°时圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,已知sin 53°=0.8;cos 53°=0.6,滑动摩擦力等于最大静摩擦力.则下列说法正确的是( )| A. | 圆环与棒间的动摩擦因数μ=0.75 | B. | 棒对环的支持力为1.6 N | ||
| C. | 重物G的质量M=0.6 kg | D. | 圆环与棒间的动摩擦因数μ=0.6 |