题目内容
 如图所示,一半径为R的半圆形光滑轨道放在水平面上,A为轨道与水平面的切点,A左边的水平面是光滑的,半圆形光滑轨道固定.一个质量为m的小球以某一速度冲上轨道,小球落地点为C.当小球将要从轨道口飞出时,轨道的压力恰好为零.
如图所示,一半径为R的半圆形光滑轨道放在水平面上,A为轨道与水平面的切点,A左边的水平面是光滑的,半圆形光滑轨道固定.一个质量为m的小球以某一速度冲上轨道,小球落地点为C.当小球将要从轨道口飞出时,轨道的压力恰好为零.求:(1)小球落地点C与A的距离.
(2)小球在A的速度大小.
(3)小球对A点的压力大小.
分析:当小球将要从轨道口飞出时,轨道的压力恰好为零,小球做圆周运动,只有重力提供向心力,因此求出这时小球的速度,小球以此速度做平抛运动,由B到C由平抛运动规律求C到A的距离,由B到A由机械能守恒定律求出A点的速度,在A点由向心力公式求小球受到的支持力,再求压力.
解答:解:(1)、设小球在B点速度为VB,轨道的压力恰好为零,只有重力提供向心力,由牛顿第二定得:mg=
,
再设小球在B运动到点C的时间为t,点C与A的距离为X,由平抛运动规律得:
X=VBt
2R=
gt2
联立以上三式 解得X=2R.
(2)、设小球在A的速度大小为VA,由机械能守恒定律得:
mVA2=
m VB2+mg×2R
代入VB解得:VA=
.
(3)、设小球受A轨道支持力大小为F,
由牛顿第二定律得:
F-mg=
代入vA 解得:F=6mg
根据牛顿第三定律得小球对A点的压力大小为6mg.
答:(1)小球落地点C与A的距离2R.
(2)小球在A的速度大小
.
(3)小球对A点的压力大小6mg.
m
| ||
| R |
再设小球在B运动到点C的时间为t,点C与A的距离为X,由平抛运动规律得:
X=VBt
2R=
| 1 |
| 2 |
联立以上三式 解得X=2R.
(2)、设小球在A的速度大小为VA,由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
代入VB解得:VA=
| 5gR |
(3)、设小球受A轨道支持力大小为F,
由牛顿第二定律得:
F-mg=
m
| ||
| R |
代入vA 解得:F=6mg
根据牛顿第三定律得小球对A点的压力大小为6mg.
答:(1)小球落地点C与A的距离2R.
(2)小球在A的速度大小
| 5gR |
(3)小球对A点的压力大小6mg.
点评:解答此题关键是分析小球的运动过程,明确小球分别在B、A的受力,选用牛顿第二定律求解,A到B的过程机械能守恒,B到C的过程做平抛运动.

练习册系列答案
相关题目
 如图所示,一半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属板,两板间的距离为d,板长为l,t=0时,磁场的磁感应强度B从B0开始均匀增大,同时,在两板中间OO′直线上的左端位置有一质量为m、带电量为+q的液滴以初速度v0水平向右射入两板间,该液滴可视为质点.(用g表示重力加速度)求:
如图所示,一半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属板,两板间的距离为d,板长为l,t=0时,磁场的磁感应强度B从B0开始均匀增大,同时,在两板中间OO′直线上的左端位置有一质量为m、带电量为+q的液滴以初速度v0水平向右射入两板间,该液滴可视为质点.(用g表示重力加速度)求: [附加题]如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的.轨道所在空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m、带正电为q的小球,为使小球刚好能到达圆环最高点;求释放点A距圆轨道最低点B的距离s.
[附加题]如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的.轨道所在空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m、带正电为q的小球,为使小球刚好能到达圆环最高点;求释放点A距圆轨道最低点B的距离s. (2013?威海模拟)如图所示,一半径为R=0.2m的竖直粗糙圆弧轨道与水平地面相接于B点,C、D两点分别位于轨道的最低点和最高点.距地面高度为h=0.45m的水平台面上有一质量为m=1kg可看作质点的物块,物块在水平向右的恒力F=4N的作用下,由静止开始运动,经过t=2s时间到达平台边缘上的A点,此时撤去恒力F,物块在空中运动至B点时,恰好沿圆弧轨道切线方向滑入轨道,物块运动到圆弧轨道最高点D时对轨道恰好无作用力.物块与平台间的动摩擦因数μ=0.2,空气阻力不计,取 g=10m/s2.求
(2013?威海模拟)如图所示,一半径为R=0.2m的竖直粗糙圆弧轨道与水平地面相接于B点,C、D两点分别位于轨道的最低点和最高点.距地面高度为h=0.45m的水平台面上有一质量为m=1kg可看作质点的物块,物块在水平向右的恒力F=4N的作用下,由静止开始运动,经过t=2s时间到达平台边缘上的A点,此时撤去恒力F,物块在空中运动至B点时,恰好沿圆弧轨道切线方向滑入轨道,物块运动到圆弧轨道最高点D时对轨道恰好无作用力.物块与平台间的动摩擦因数μ=0.2,空气阻力不计,取 g=10m/s2.求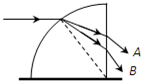 如图所示,一半径为R的
如图所示,一半径为R的