题目内容
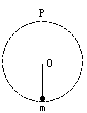
轻绳一端固定在光滑水平轴O上，另一端系一质量为m的小球，如图所示，在最低点给小球一初速度，使其在竖直平面内做圆周运动，且刚好能通过最高点P．下列说法正确的是( )
| A．小球在最高点时对绳的拉力为零 |
| B．小球在最高点时对绳的拉力大小为mg |
| C．若增大小球的初速度，则过最高点时球对绳的力一定增大 |
| D．若增大小球的初速度，则在最低点时球对绳的力一定增大 |
ACD
以小球为研究对象，设在最高点时杆对小球的作用力大小为F，方向竖直向上．小球刚好能通过最高点P，速度为零，根据牛顿第二定律得，mg-F=m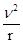
=0，即有F=mg，再由牛顿第三定律得到，小球在最高点时对杆的作用力也为mg，方向竖直向下;
对于球，在最高点时：若v＜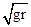
时，杆对球的作用力方向竖直向上时，由上得到F=mg-m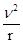，增大小球的初速度，杆对球的作用力F减小，则球对杆的力减小．
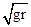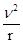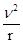若v＞时，杆对球的作用力方向竖直向下时，由mg+F=m，得F=m-mg，当速度v增大时，杆对球的作用力F增大，则球对杆的力增大．
本题属于竖直平面内圆周运动临界条件问题，抓住杆能支撑小球的特点，由牛顿第二定律进行分析．
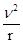=0，即有F=mg，再由牛顿第三定律得到，小球在最高点时对杆的作用力也为mg，方向竖直向下;对于球，在最高点时：若v＜
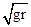时，杆对球的作用力方向竖直向上时，由上得到F=mg-m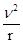，增大小球的初速度，杆对球的作用力F减小，则球对杆的力减小．若v＞
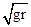时，杆对球的作用力方向竖直向下时，由mg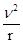+F=m，得F=m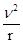-mg，当速度v增大时，杆对球的作用力F增大，则球对杆的力增大．本题属于竖直平面内圆周运动临界条件问题，抓住杆能支撑小球的特点，由牛顿第二定律进行分析．
练习册系列答案
阅读快车系列答案
相关题目
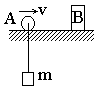
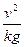
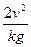
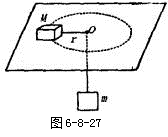
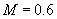kg的物体，静止于水平面，另一端通过光滑小孔吊着质量
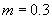kg的物体，M的中点与圆孔距离为0.2m，并知M和水平面的最大静摩擦力为2N，现使此平面绕中心轴线转动，问角速度
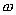在什么范围m会处于静止状态？（
）
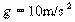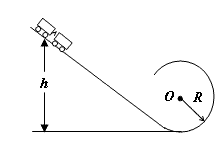
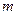的汽车以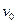
的速度安全驶过半径为
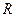的凸形桥的桥顶，这时汽车对桥顶的压力是_________，汽车此时所需的向心力是汽车所受支持力和__________的合力，汽车能安全通过桥顶的最大行驶速度不能超过_____________ (重力加速度为g)