题目内容
(1)已知地球质量为M,引力常量为G,在地心-恒星坐标系中,地球自转周期为T.求同步卫星离地心的距离.
(2)已知地球半径为R,在地心-恒星坐标系中,地球自转周期为T,贴近地球运行的卫星的周期为T0.求同步卫星离地心的距离.
(3)已知地球半径为R,地面附近引力场强度约等于地面附近重力加速度g,在地心-恒星坐标系中地球自转周期为T.求同步卫星离地心的距离.
(2)已知地球半径为R,在地心-恒星坐标系中,地球自转周期为T,贴近地球运行的卫星的周期为T0.求同步卫星离地心的距离.
(3)已知地球半径为R,地面附近引力场强度约等于地面附近重力加速度g,在地心-恒星坐标系中地球自转周期为T.求同步卫星离地心的距离.
地球对同步卫星的万有引力提供同步卫星绕地球做圆周运的向心力,
设同步卫星离地心的距离为r,同步卫星的质量为m,
同步卫星绕地球做运转运动的周期等于地球自转周期T;
(1)由牛顿第二定律得:G
=m(
)2r,解得:r=
;
(2)由牛顿第二定律得:
对同步卫星:G
=m(
)2r,
对贴近地球运行的卫星:G
=m′(
)2R,
解得:r=
R;
(3)由牛顿第二定律得:G
=m(
)2r,
在地球表面的物体受到的重力等于地球对它的万有引力,
即:G
=m′g,
解得:r=
;
答:(1)同步卫星离地心的距离为
;(2)同步卫星离地心的距离为
R;(3)同步卫星离地心的距离为
.
设同步卫星离地心的距离为r,同步卫星的质量为m,
同步卫星绕地球做运转运动的周期等于地球自转周期T;
(1)由牛顿第二定律得:G
| Mm |
| r2 |
| 2π |
| T |
| 3 |
| ||
(2)由牛顿第二定律得:
对同步卫星:G
| Mm |
| r2 |
| 2π |
| T |
对贴近地球运行的卫星:G
| Mm′ |
| R2 |
| 2π |
| T0 |
解得:r=
| 3 |
| ||||
(3)由牛顿第二定律得:G
| Mm |
| r2 |
| 2π |
| T |
在地球表面的物体受到的重力等于地球对它的万有引力,
即:G
| Mm′ |
| R2 |
解得:r=
| 3 |
| ||
答:(1)同步卫星离地心的距离为
| 3 |
| ||
| 3 |
| ||||
| 3 |
| ||

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目


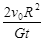
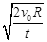 的速度就可能离开月球表面围绕月球做圆周运动
的速度就可能离开月球表面围绕月球做圆周运动