题目内容
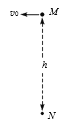
【题目】如图所示, MN为同一竖直线上相距为h的两点,空间存在竖直平面内方向未知的匀强电场。一带电小球(m、+q)从M点以速度v0=![]() 水平抛出,刚好能够通过N点,过N点时速度大小v=2
水平抛出,刚好能够通过N点,过N点时速度大小v=2![]() ,重力加速度为g,则( )
,重力加速度为g,则( )
A.小球从M到N点动能变化量为3mgh
B.电场强度E=![]()
C.小球从M到N点用时t=![]()
D.小球从M到N点用时t=![]()
【答案】ABD
【解析】
A.根据动能定理可得小球从M到N点动能变化量为:![]() ,解得:
,解得:
△Ek=3mgh
故A符合题意。
BCD.将小球的运动分解为水平方向的运动与竖直方向的运动,由于竖直方向重力与电场力都做正功,可知在竖直方向电场力的分量竖直向下;由于N点恰好在M点的正下方,选择竖直方向为y方向,水平方向为x方向,则电场力沿水平方向的分量不做功,所以:W=Fyh,根据动能定理得:W+mgh=![]() mv2﹣
mv2﹣![]() mv02,解得电场力沿竖直方向的分量为:
mv02,解得电场力沿竖直方向的分量为:
Fy=2mg
小球沿竖直方向的加速度为:![]() ,根据
,根据![]() 得小球运动的时间为:
得小球运动的时间为:![]()
小球到达N点时沿竖直方向的分速度为:vy=ayt=![]() ,小球沿水平方向的分速度为:
,小球沿水平方向的分速度为:![]() 。在水平方向上根据动量定理有:Fxt=mvx=mv0。所以有:
。在水平方向上根据动量定理有:Fxt=mvx=mv0。所以有:
Fx=2![]() mg
mg
则小球受到的电场力为:![]() ,所以电场强度为:
,所以电场强度为:
![]()
故BD符合题意,C不符合题意。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目