��Ŀ����
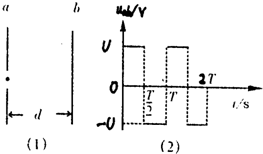 ��ͼ��1����ʾ��������㹻�����������ƽ�еĽ�����a��b֮��ľ���Ϊd������֮��ĵ�ѹ����ͼ��2����ʾ�Ĺ����������Եı仯����a��b���Ƹ�ʱ����ѹΪ������a��b���Ƶ�ʱ����ѹΪ���������ѹ�仯����ΪT����ѹ�����ֵΪU��һ������Ϊm�������Ϊq�Ĵ��������ӣ��������ƣ��ڵ糡���������£���t=
��ͼ��1����ʾ��������㹻�����������ƽ�еĽ�����a��b֮��ľ���Ϊd������֮��ĵ�ѹ����ͼ��2����ʾ�Ĺ����������Եı仯����a��b���Ƹ�ʱ����ѹΪ������a��b���Ƶ�ʱ����ѹΪ���������ѹ�仯����ΪT����ѹ�����ֵΪU��һ������Ϊm�������Ϊq�Ĵ��������ӣ��������ƣ��ڵ糡���������£���t=| T | 6 |
��1������������֮��ļ��ٶȴ�СΪ���
��2��������������֮���˶�һ������Tʱ������a��ľ���Ϊ���٣�����֪���Ӳ����������������
����������ţ�ٵڶ���������ٶȣ������ӵ��˶��ֶ��о����ֱ�������ε�λ�ƣ����������ȼ��ٺ��ȼ����˶��ĶԳ�������ٵ�λ�ƣ�
����⣺��1�������ӵļ��ٶȴ�СΪa���У�
qE=ma
����E=
�����ã�a=
��2��������
��
�������ȼ��٣���
X1=
a(
)2=
������
-
�������ȼ��ٵ��ٶ�Ϊ�㣬��
X2=X1=
-
�ڷ��������ȼ��٣���
X3=
a(
)2=
������
-
�ڷ��������ȼ��ٵ��ٶ�Ϊ�㣬��
X4=X3
�������Ӿ�a�����Ϊ��
X=X1+X2-X3-X4=
�𣺣�1������������֮��ļ��ٶȴ�СΪ
��2��������������֮���˶�һ������Tʱ������a��ľ���Ϊ
qE=ma
����E=
| U |
| d |
�����ã�a=
| qU |
| md |
��2��������
| T |
| 6 |
| T |
| 2 |
X1=
| 1 |
| 2 |
| 2T |
| 6 |
| qUT2 |
| 18md |
������
| 3T |
| 6 |
| 5T |
| 6 |
X2=X1=
| qUT2 |
| 18md |
| 5T |
| 6 |
| 6T |
| 6 |
X3=
| 1 |
| 2 |
| T |
| 6 |
| qUT2 |
| 72md |
������
| 6T |
| 6 |
| 7T |
| 6 |
X4=X3
�������Ӿ�a�����Ϊ��
X=X1+X2-X3-X4=
| qUT2 |
| 12md |
�𣺣�1������������֮��ļ��ٶȴ�СΪ
| qU |
| md |
��2��������������֮���˶�һ������Tʱ������a��ľ���Ϊ
| qUT2 |
| 12md |
������������ѵ��������ӵ��˶��м����м��٣�ע��Ӧ���˶��ĶԳ�����λ�ƿ��Լ����㣮

��ϰ��ϵ�д�
 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�����Ŀ
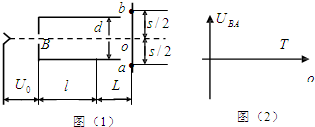 ��ͼ��1����ʾΪʾ�����IJ��ֹ��죮������е缫 K �������ϵķ�����ӣ����ٲ��ƣ���������ѹΪU0 �ļ��ٵ糡����AС�� f ��ˮƽ������ A��B ����������������䣬�� k f ��Ϊ l��������� d�����Ӵ����������ӫ���� �ϣ����������Ե�ľ���Ϊ L�����ϵ��е�Ϊ O������ a��b ���㵽�� O �ľ����Ϊ s������ A��B �������ϱ仯�ĵ�ѹ����ÿ������ͨ������ļ���ʱ���ڣ��糡�������㶨�ģ���Ҫ�� t=0 ʱ�����������ĵ��ӳ�ƫת�糡��������ϵ� a �㣬Ȼ��ʱ��T �����������Ƶ� b �㣬�������γ�һ����ֱ���ߣ����ӵĵ���Ϊ e������Ϊ m��
��ͼ��1����ʾΪʾ�����IJ��ֹ��죮������е缫 K �������ϵķ�����ӣ����ٲ��ƣ���������ѹΪU0 �ļ��ٵ糡����AС�� f ��ˮƽ������ A��B ����������������䣬�� k f ��Ϊ l��������� d�����Ӵ����������ӫ���� �ϣ����������Ե�ľ���Ϊ L�����ϵ��е�Ϊ O������ a��b ���㵽�� O �ľ����Ϊ s������ A��B �������ϱ仯�ĵ�ѹ����ÿ������ͨ������ļ���ʱ���ڣ��糡�������㶨�ģ���Ҫ�� t=0 ʱ�����������ĵ��ӳ�ƫת�糡��������ϵ� a �㣬Ȼ��ʱ��T �����������Ƶ� b �㣬�������γ�һ����ֱ���ߣ����ӵĵ���Ϊ e������Ϊ m��