题目内容
(1)如图(1)所示,一根水平张紧弹性长绳上有等间距的O、P、Q质点,相邻两质点间距离为1.0m.t=0时刻O质点从平衡位置开始沿y轴方向振动,并产生沿x轴正方向传播的波,O质点的振动图象如图(2)所示.当O质点第一次达到正向最大位移时,P质点刚开始振动,则
A.质点Q的起振方向为y轴正向
B.P、Q两质点之间的距离为半个波长
C.这列波传播的速度为1.0m/s
D.在一个周期内,质点O通过的路程为0.4m
(2)如图(3)所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=
.一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.试求:?
①该单色光在玻璃砖中的传播速度.?
②玻璃砖的厚度d.

AC
AC
A.质点Q的起振方向为y轴正向
B.P、Q两质点之间的距离为半个波长
C.这列波传播的速度为1.0m/s
D.在一个周期内,质点O通过的路程为0.4m
(2)如图(3)所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=
| 2 |
①该单色光在玻璃砖中的传播速度.?
②玻璃砖的厚度d.

分析:(1)质点的起振方向与波源的起振方向相同,当O质点第一次达到正向最大位移时,P质点刚开始振动,结合振动图象可以得出周期和波长,从而求出波速.
(2)根据v=
求出光在介质中传播的速度.
光首先在玻璃砖的上表面发生反射打在光屏上,在上表面折射后射到下表面的光发生反射在上表面再次折射打在光屏上,根据AB两点的距离,通过折射率的公式,结合几何关系求出玻璃砖的厚度.
(2)根据v=
| c |
| n |
光首先在玻璃砖的上表面发生反射打在光屏上,在上表面折射后射到下表面的光发生反射在上表面再次折射打在光屏上,根据AB两点的距离,通过折射率的公式,结合几何关系求出玻璃砖的厚度.
解答:解:(1)A、质点的起振方向与波源的起振方向相同,所以Q质点的起振方向与O点的起振方向相同.故A正确.
B、当O质点第一次达到正向最大位移时,P质点刚开始振动,知OP间的距离等于
,则P、Q两质点之间的距离为
.故B错误.
C、
=1m,则λ=4m.T=4s,所以波速v=
=
m/s=1m/s.故C正确.
D、一个周期内质点振动的路程等于4A,所以质点O通过的路程为0.2m.故D错误.
故选AC.
(2)①由折射率公式 n=
解得 v=
=
×108m/s?
故光在玻璃砖中传播的速度为
×108m/s.
②由折射率公式 n=
解得sinθ2=
,θ2=30°.
作出如右图所示的光路,△CDE为等边三角形,四边形ABEC为梯形,CE=AB=h.玻璃的厚度d就是边长h的等边三角形的高.
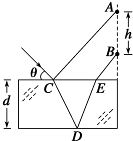
d=hcos30°=
h=1.732cm.
故玻璃砖的厚度d为1.732cm.
B、当O质点第一次达到正向最大位移时,P质点刚开始振动,知OP间的距离等于
| λ |
| 4 |
| λ |
| 4 |
C、
| λ |
| 4 |
| λ |
| T |
| 4 |
| 4 |
D、一个周期内质点振动的路程等于4A,所以质点O通过的路程为0.2m.故D错误.
故选AC.
(2)①由折射率公式 n=
| c |
| v |
| c |
| n |
3
| ||
| 2 |
故光在玻璃砖中传播的速度为
3
| ||
| 2 |
②由折射率公式 n=
| sinθ1 |
| sinθ2 |
| 1 |
| 2 |
作出如右图所示的光路,△CDE为等边三角形,四边形ABEC为梯形,CE=AB=h.玻璃的厚度d就是边长h的等边三角形的高.

d=hcos30°=
| ||
| 2 |
故玻璃砖的厚度d为1.732cm.
点评:解决本题的关键质点振动与波动的联系,以及掌握光的折射率公式n=
,n=
.
| c |
| v |
| sinθ1 |
| sinθ2 |

练习册系列答案
相关题目
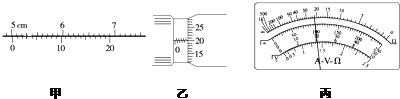
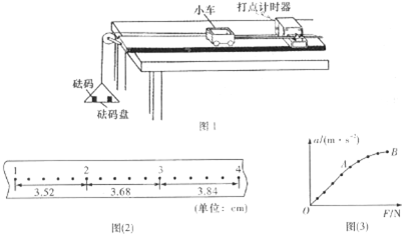
 (1)如图(1)所示,在验证动量守恒的实验中:
(1)如图(1)所示,在验证动量守恒的实验中:

