题目内容
(1)如图(1)所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形,质点P的振动图象如图(2)所示,则这列波的传播速度为
(2)如图(3)所示,一个截面为直角三角形的玻璃砖放在水平地面上,折射率n=
.入射光线垂直于AB边从F点射人玻璃砖,经E点折射后到达地面上的P点,已知AE=ED=L,∠ABD=60°,试求光线从F到P所用时间.(光在真空中的速度大小为c)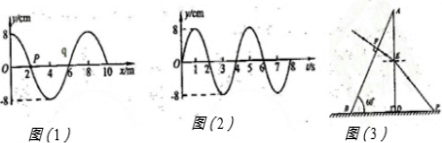
2m/s
2m/s
m/s,平衡位置在6m处的q点的振动方程为y=-8sin(
t )
| π |
| 2 |
-8sin(
t )
cm.| π |
| 2 |
(2)如图(3)所示,一个截面为直角三角形的玻璃砖放在水平地面上,折射率n=
| 2 |

分析:(1)由波动图象(1)读出波长λ,由振动图象(2)读出周期T,由公式v=
得到波速v.p与q是反相点,两者位移始终相反.
(2)入射光线垂直于AB边从F点方向不变射人玻璃砖,由几何知识确定光线在直角边AD的入射角,由折射定律求出折射角,由v=
求出光在玻璃砖中传播速度.由几何关系求解光传播路程,再求出光线从F到P所用时间.
| λ |
| T |
(2)入射光线垂直于AB边从F点方向不变射人玻璃砖,由几何知识确定光线在直角边AD的入射角,由折射定律求出折射角,由v=
| c |
| n |
解答: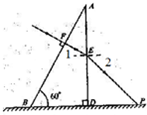 解:
解:
(1)由波动图象(1)读出波长λ=8m,由振动图象(2)读出周期T=4s,由公式v=
得到波速v=2m/s.
由于p与q平衡位置间距离相距半个波长,是反相点,两者位移始终相反.则q点的振动方程为y=-8sin(
t )cm.
(2)在ED边上,∠1=30°.根据折射定律得
=n 得到∠2=45°
由几何知识得,EP=
=
L FE=AEsin30°=
又 n=
光在玻璃砖里传播时间 t1=
光从E传到P的时间 t2=
则t=t1+ t2 =
.
故答案为:
(1)2m/s;-8sin(
t )cm.
(2)光线从F到P所用时间为
.
 解:
解:(1)由波动图象(1)读出波长λ=8m,由振动图象(2)读出周期T=4s,由公式v=
| λ |
| T |
由于p与q平衡位置间距离相距半个波长,是反相点,两者位移始终相反.则q点的振动方程为y=-8sin(
| π |
| 2 |
(2)在ED边上,∠1=30°.根据折射定律得
| sin∠2 |
| sin∠1 |
由几何知识得,EP=
| ED |
| sin45° |
| 2 |
| L |
| 2 |
又 n=
| c |
| v |
光在玻璃砖里传播时间 t1=
| FE |
| v |
光从E传到P的时间 t2=
| EP |
| c |
则t=t1+ t2 =
3
| ||
| 2c |
故答案为:
(1)2m/s;-8sin(
| π |
| 2 |
(2)光线从F到P所用时间为
3
| ||
| 2c |
点评:对于几何光学,关键是作出光路图,往往运用几何研究角度与距离.比较简单.

练习册系列答案
相关题目
 (1)如图(1)所示,在验证动量守恒的实验中:
(1)如图(1)所示,在验证动量守恒的实验中:

