��Ŀ����
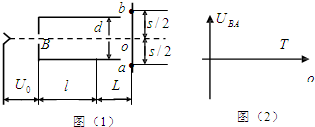 ��ͼ��1����ʾΪʾ�����IJ��ֹ��죮������е缫 K �������ϵķ�����ӣ����ٲ��ƣ���������ѹΪU0 �ļ��ٵ糡����AС�� f ��ˮƽ������ A��B ����������������䣬�� k f ��Ϊ l��������� d�����Ӵ����������ӫ���� �ϣ����������Ե�ľ���Ϊ L�����ϵ��е�Ϊ O������ a��b ���㵽�� O �ľ����Ϊ s������ A��B �������ϱ仯�ĵ�ѹ����ÿ������ͨ������ļ���ʱ���ڣ��糡�������㶨�ģ���Ҫ�� t=0 ʱ�����������ĵ��ӳ�ƫת�糡��������ϵ� a �㣬Ȼ��ʱ��T �����������Ƶ� b �㣬�������γ�һ����ֱ���ߣ����ӵĵ���Ϊ e������Ϊ m��
��ͼ��1����ʾΪʾ�����IJ��ֹ��죮������е缫 K �������ϵķ�����ӣ����ٲ��ƣ���������ѹΪU0 �ļ��ٵ糡����AС�� f ��ˮƽ������ A��B ����������������䣬�� k f ��Ϊ l��������� d�����Ӵ����������ӫ���� �ϣ����������Ե�ľ���Ϊ L�����ϵ��е�Ϊ O������ a��b ���㵽�� O �ľ����Ϊ s������ A��B �������ϱ仯�ĵ�ѹ����ÿ������ͨ������ļ���ʱ���ڣ��糡�������㶨�ģ���Ҫ�� t=0 ʱ�����������ĵ��ӳ�ƫת�糡��������ϵ� a �㣬Ȼ��ʱ��T �����������Ƶ� b �㣬�������γ�һ����ֱ���ߣ����ӵĵ���Ϊ e������Ϊ m����1���� A��B ���ѹ�����ֵ��
��2���Ƶ������� A��B �����ĵ�ѹUBA �� t �Ĺ�ϵʽ��
��3����ͼ��2���л��� 0-T �ڵ�UBA-t ͼ��ʾ��ͼ��
��������1�����Ӿ����ٵ糡���٣�����ƫת�糡������ƽ���˶������糡������ֱ���˶��������˶�ѧ��ʽ��ϵ��Ӵ�ƫת�糡���������U����Ӷ������ƫת�糡������O�������ͨ�����ι�ϵ���ƫת��ѹ������ƫ�����Ĺ�ϵ��
��2����t=0���������ĵ��Ӵ������ϵ�b�㣬Ȼ����ʱ��T�������������Ƶ�a�㣬������������ϵ�ƫ������ʱ��Ĺ�ϵ���Ӷ���ϵڣ�1�����еĽ������U��ʱ��Ĺ�ϵ��
��3������U��t�Ĺ�ϵʽ����U-tͼ��
��2����t=0���������ĵ��Ӵ������ϵ�b�㣬Ȼ����ʱ��T�������������Ƶ�a�㣬������������ϵ�ƫ������ʱ��Ĺ�ϵ���Ӷ���ϵڣ�1�����еĽ������U��ʱ��Ĺ�ϵ��
��3������U��t�Ĺ�ϵʽ����U-tͼ��
���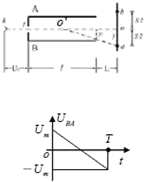 �⣺��1������Ӿ�U0���ٺ���ٶ�Ϊv0�����ݶ��ܶ����ã�
�⣺��1������Ӿ�U0���ٺ���ٶ�Ϊv0�����ݶ��ܶ����ã�
eU0=
m
��
�����ƫת�ɳ��糡��ˮƽ����ļн�Ϊ�գ�
��ƫת�糡�У���ǿE=
���ٶ�a=
=
��
�˶�ʱ��Ϊ t1=
��
ƫתλ��y1=
a
��
tan��=
=
����
�����ã�y1=
����
tan��=
����
��tan��=
����x=
���Ե��Ӵ�ƫת�糡���������U����Ӷ������ƫת�糡������O���������ͼ���ɼ��ι�ϵ�ã�
=
��
��y=
=
��
ȡy=
����A��B���ѹ�����ֵUAB=
��
��2�������������Ƶ��ٶ�Ϊ v=
��11��
�ɢ�ã�UAB=
��
s-vt��=
��
s-
t�� ��12����
��3������ʽ��12���ã���ͼ��ʾUBA-t ͼ��ʾ��ͼ��ͼ��ʾ������UAB=
��
��
��1��AB��������ӵ�ѹ�����ֵΪ
��
��2������AB������ѹU��ʱ��t��0��t��T���Ĺ�ϵʽΪUAB=
��
s-
t����
��3����ͼ��ʾUBA-t ͼ��ʾ��ͼ��ͼ��ʾ������UAB=
��
 �⣺��1������Ӿ�U0���ٺ���ٶ�Ϊv0�����ݶ��ܶ����ã�
�⣺��1������Ӿ�U0���ٺ���ٶ�Ϊv0�����ݶ��ܶ����ã�eU0=
| 1 |
| 2 |
| v | 2 0 |
�����ƫת�ɳ��糡��ˮƽ����ļн�Ϊ�գ�
��ƫת�糡�У���ǿE=
| U |
| d |
���ٶ�a=
| eE |
| m |
| eU |
| md |
�˶�ʱ��Ϊ t1=
| l |
| v0 |
ƫתλ��y1=
| 1 |
| 2 |
| t | 2 1 |
tan��=
| vy |
| v0 |
| at |
| v0 |
�����ã�y1=
| Ul2 |
| 4dU0 |
tan��=
| Ul |
| 2dU0 |
��tan��=
| y1 |
| x |
| l |
| 2 |
���Ե��Ӵ�ƫת�糡���������U����Ӷ������ƫת�糡������O���������ͼ���ɼ��ι�ϵ�ã�
| y |
| y1 |
| L+0.5l |
| 0.5l |
��y=
| (2L+l)y1 |
| l |
| (2L+l)Ul |
| 4dU0 |
ȡy=
| s |
| 2 |
| 2dU0s |
| (2L+l)l |
��2�������������Ƶ��ٶ�Ϊ v=
| s |
| T |
�ɢ�ã�UAB=
| 4dU0 |
| (2L+l)l |
| 1 |
| 2 |
| 4dU0 |
| (2L+l)l |
| 1 |
| 2 |
| s |
| T |
��3������ʽ��12���ã���ͼ��ʾUBA-t ͼ��ʾ��ͼ��ͼ��ʾ������UAB=
| 2dU0s |
| (2L+l)l |
��
��1��AB��������ӵ�ѹ�����ֵΪ
| 2dU0s |
| (2L+l)l |
��2������AB������ѹU��ʱ��t��0��t��T���Ĺ�ϵʽΪUAB=
| 4dU0 |
| (2L+l)l |
| 1 |
| 2 |
| s |
| T |
��3����ͼ��ʾUBA-t ͼ��ʾ��ͼ��ͼ��ʾ������UAB=
| 2dU0s |
| (2L+l)l |
�������������Ĺؼ�������������������е��˶�����������˶�ѧ��ʽ���ţ�ٵڶ��������ƫ������ͨ��ƫ������ƫת��ѹ�Ĺ�ϵ���ó�U��t�Ĺ�ϵʽ��

��ϰ��ϵ�д�
�����Ŀ


 ��ʼ���з���ĵ���
��ʼ���з���ĵ���