��Ŀ����
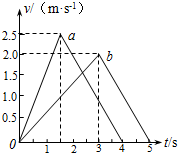 �����������ֱ�Ϊm1��m2������A��B�����ŷ���ˮƽ�����ϣ�����ͬ��ˮƽ����F1��F2�ֱ�����������A��B�ϣ�����һ��ʱ���ȥ����������Ի���һ�ξ����ֹͣ��A��B�������˶���v-tͼ��ֱ���a��bͼ����ʾ����ͼ����Ϣ���Եó���������
�����������ֱ�Ϊm1��m2������A��B�����ŷ���ˮƽ�����ϣ�����ͬ��ˮƽ����F1��F2�ֱ�����������A��B�ϣ�����һ��ʱ���ȥ����������Ի���һ�ξ����ֹͣ��A��B�������˶���v-tͼ��ֱ���a��bͼ����ʾ����ͼ����Ϣ���Եó�������������������ˮƽ����F1��F2�Ĵ�С��ϵδ֪����Ҫ��Ħ������ֻ�ܸ��ݳ�����������˶�������з�����Ҫ�Ƚ�Ħ���������������Ĺ��Ķ��٣�һ��Ҫ֪��������λ�ƵĴ�С��ϵ������ͼ������������ͬ�������δ����ǰ���ٶȵĹ�ϵ�ٱȽ������Ĵ�С������ʶ�Ӧ����ٶȣ���Ӧ���������ͬʱ�����ľ���ֵ��
����⣺��m1=m2����f1=f2��
���ݶ��ܶ�����a��
WF1-f1s1=0
ͬ����b��
WF2-f2s2=0
��s1=4��2.5��
=5.0m
s2=2��5��
=5.0m
��WF1=WF2����A����
������������������ٶ�ͼ��ƽ�У��ʼ��ٶȴ�С��ȣ�����������ˮƽ����Ķ�Ħ�����طֱ�Ϊ��1����2��
��a1=a2=��g=1m/s2
���1=��2=
=0.1��
�����Ϸ�����֪F1=m1��a1+��1g��=m1��
��
������F1�����˲ʱ����P1=
m1
ͬ��F2=m2��a2+��2g��=
m2
������F2�����˲ʱ����P2=
m2
��P1=2P2 ��C��ȷ��
��m1=2m2����f1=
f2��
���ݶ��ܶ�����a��
WF1-f1s1=0
ͬ����b��
WF2-f2s2=0
��s1=4��2.5��
=5.0m
s2=2��5��
=5.0m
��WF1=
WF2����B��ȷ��
������������������ٶ�ͼ��ƽ�У��ʼ��ٶȴ�С��ȣ�����������ˮƽ����Ķ�Ħ�����طֱ�Ϊ��1����2��
��a1=a2=��g=1m/s2
���1=��2=
=0.1��
�����Ϸ�����֪F1=m1��a1+��1g��=m1��
��
������F1�����˲ʱ����P1=
m1
ͬ��F2=m2��a2+��2g��=
m2
������F2�����˲ʱ����P2=
m2
��m1=2m2��
��P1=4P2����D����
��ѡB��C��
���ݶ��ܶ�����a��
WF1-f1s1=0
ͬ����b��
WF2-f2s2=0
��s1=4��2.5��
| 1 |
| 2 |
s2=2��5��
| 1 |
| 2 |
��WF1=WF2����A����
������������������ٶ�ͼ��ƽ�У��ʼ��ٶȴ�С��ȣ�����������ˮƽ����Ķ�Ħ�����طֱ�Ϊ��1����2��
��a1=a2=��g=1m/s2
���1=��2=
| 1 |
| 10 |
�����Ϸ�����֪F1=m1��a1+��1g��=m1��
| 8 |
| 3 |
������F1�����˲ʱ����P1=
| 20 |
| 3 |
ͬ��F2=m2��a2+��2g��=
| 5 |
| 3 |
������F2�����˲ʱ����P2=
| 10 |
| 3 |
��P1=2P2 ��C��ȷ��
��m1=2m2����f1=
| 1 |
| 2 |
���ݶ��ܶ�����a��
WF1-f1s1=0
ͬ����b��
WF2-f2s2=0
��s1=4��2.5��
| 1 |
| 2 |
s2=2��5��
| 1 |
| 2 |
��WF1=
| 1 |
| 2 |
������������������ٶ�ͼ��ƽ�У��ʼ��ٶȴ�С��ȣ�����������ˮƽ����Ķ�Ħ�����طֱ�Ϊ��1����2��
��a1=a2=��g=1m/s2
���1=��2=
| 1 |
| 10 |
�����Ϸ�����֪F1=m1��a1+��1g��=m1��
| 8 |
| 3 |
������F1�����˲ʱ����P1=
| 20 |
| 3 |
ͬ��F2=m2��a2+��2g��=
| 5 |
| 3 |
������F2�����˲ʱ����P2=
| 10 |
| 3 |
��m1=2m2��
��P1=4P2����D����
��ѡB��C��
�����������ۺ��Ժ�ǿ��������������ţ�ٵڶ����ɣ����ܶ��������ʵ�˲ʱֵ����ʽ�������v-tͼ�����ٶȣ�λ�����ܷ�ɹ�����Ĺؼ���

��ϰ��ϵ�д�
 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
�����Ŀ
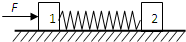 ��ͼ��ʾ����һ�ֲ�ˮƽ���������������ֱ�Ϊm1��m2��ľ��1��2���м���һԭ��ΪL������ϵ��Ϊk���ᵯ������������ľ����ˮƽ���Ķ�Ħ��������Ϊ�̣�����ˮƽ���ҵ���F��ľ��1������ľ��һ�����������˶�ʱ����ľ��֮��ľ���Ϊ��������
��ͼ��ʾ����һ�ֲ�ˮƽ���������������ֱ�Ϊm1��m2��ľ��1��2���м���һԭ��ΪL������ϵ��Ϊk���ᵯ������������ľ����ˮƽ���Ķ�Ħ��������Ϊ�̣�����ˮƽ���ҵ���F��ľ��1������ľ��һ�����������˶�ʱ����ľ��֮��ľ���Ϊ��������A��L+
| ||
B��L+
| ||
C��L-
| ||
D��L-
|
 ��ͼ��ʾ����һ�ֲ�ˮƽ���������������ֱ�Ϊm1��m2��ľ���м���һԭ��ΪL������ϵ��ΪK���ᵯ������������ľ��������Ļ���Ħ��������Ϊ�̣�����һ��ˮƽ����ɦȵ���F������m1����ͼ��ʾ������ľ��һ�������ص��������˶�ʱ�������α��ڵ������ڣ�������֮��ľ����ǣ�������
��ͼ��ʾ����һ�ֲ�ˮƽ���������������ֱ�Ϊm1��m2��ľ���м���һԭ��ΪL������ϵ��ΪK���ᵯ������������ľ��������Ļ���Ħ��������Ϊ�̣�����һ��ˮƽ����ɦȵ���F������m1����ͼ��ʾ������ľ��һ�������ص��������˶�ʱ�������α��ڵ������ڣ�������֮��ľ����ǣ�������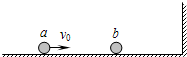 ��2008?���ݶ�ģ����ͼ��ʾ���⻬ˮƽ���������������ֱ�Ϊm1��m2��С��a��b����a��ˮƽ�ٶ�vo=1m/s���������˶�����b���ھ�ֹ״̬�������Ҳ���һ��ֱǽ�ڣ���������֮�䡢����ǽ��֮�䷢������ʱ����е����ʧ��Ϊ��ʹ�����ܷ���������ֻ�ܷ���������ײ�����������������֮��m1/m2Ӧ����ʲô������
��2008?���ݶ�ģ����ͼ��ʾ���⻬ˮƽ���������������ֱ�Ϊm1��m2��С��a��b����a��ˮƽ�ٶ�vo=1m/s���������˶�����b���ھ�ֹ״̬�������Ҳ���һ��ֱǽ�ڣ���������֮�䡢����ǽ��֮�䷢������ʱ����е����ʧ��Ϊ��ʹ�����ܷ���������ֻ�ܷ���������ײ�����������������֮��m1/m2Ӧ����ʲô������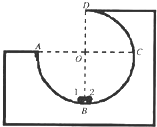 ��ͼ��ʾ����ˮƽ���Ϲ̶�һ���뾶R=1m��3/4�⻬Բ������Ĺ�������Բ����O�㣬AOC����ˮƽ��BOD������ֱ����Բ�ܹ������͵�B�����������ֱ�Ϊm1=4kg��m 2=1kg�Ŀ���Ϊ�ʵ��С��1��2����С������һ�����̵��ᵯ�ɣ������ɴ�����EP=90J�ĵ�������ʱ�������ɣ�ijʱ�̽�����������ɽ�����С�����������ٶ�g=10m/s2������
��ͼ��ʾ����ˮƽ���Ϲ̶�һ���뾶R=1m��3/4�⻬Բ������Ĺ�������Բ����O�㣬AOC����ˮƽ��BOD������ֱ����Բ�ܹ������͵�B�����������ֱ�Ϊm1=4kg��m 2=1kg�Ŀ���Ϊ�ʵ��С��1��2����С������һ�����̵��ᵯ�ɣ������ɴ�����EP=90J�ĵ�������ʱ�������ɣ�ijʱ�̽�����������ɽ�����С�����������ٶ�g=10m/s2������