题目内容
 如图所示,在一粗糙水平面上有两个质量分别为m1和m2的木块中间用一原长为L、劲度系数为K的轻弹簧连接起来,木块与地面间的滑动摩擦因数均为μ,现用一与水平方向成θ的力F作用在m1上如图所示,问两木块一起向左沿地面匀速运动时(弹簧形变在弹性限度内),它们之间的距离是( )
如图所示,在一粗糙水平面上有两个质量分别为m1和m2的木块中间用一原长为L、劲度系数为K的轻弹簧连接起来,木块与地面间的滑动摩擦因数均为μ,现用一与水平方向成θ的力F作用在m1上如图所示,问两木块一起向左沿地面匀速运动时(弹簧形变在弹性限度内),它们之间的距离是( )分析:当两物体匀速直线运动时:物体间的距离就等于弹簧的原长加上形变量,对m1,m2受力分析求出弹力,应用胡克定律求出形变量和原长相加.
解答:解:对m2受力分析如图:
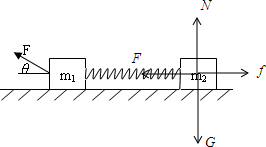
由平衡条件:
F=f=μN=μG=μm2g
由胡克定律:F=kx
得:x=
所以距离为:L+
对m1受力分析并分解如图:
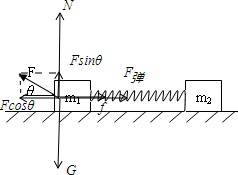
由平衡条件:N=G-Fsinθ=m1g-Fsinθ
F弹=Fcosθ-f=Fcosθ-μ(m1g-Fsinθ)
由胡克定律:F=kx
得:x=
所以距离为:L+
综上所述:距离为:L+
或L+
故选:B

由平衡条件:
F=f=μN=μG=μm2g
由胡克定律:F=kx
得:x=
| μm2g |
| k |
所以距离为:L+
| μm2g |
| k |
对m1受力分析并分解如图:

由平衡条件:N=G-Fsinθ=m1g-Fsinθ
F弹=Fcosθ-f=Fcosθ-μ(m1g-Fsinθ)
由胡克定律:F=kx
得:x=
| Fcosθ-μ(m1g-Fsinθ) |
| k |
所以距离为:L+
| Fcosθ-μ(m1g-Fsinθ) |
| k |
综上所述:距离为:L+
| μm2g |
| k |
| Fcosθ-μ(m1g-Fsinθ) |
| k |
故选:B
点评:两物体受力平衡,分别受力分析列式即可,需要注意弹簧的弹力为任一端受到的拉力,不要把两端受的拉力加起来当弹力.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 (2013?湛江一模)如图所示,在一根粗糙的水平直杆上,套有两个质量均为m的铁环,两铁环上系着两根等长线共同拴住质量为M的小球,两铁环与小球都处于静止状态.现想办法使得两铁环间距离AB增大一些而同时仍能保持系统平衡,则OA绳和OB绳的拉力变化情况是( )
(2013?湛江一模)如图所示,在一根粗糙的水平直杆上,套有两个质量均为m的铁环,两铁环上系着两根等长线共同拴住质量为M的小球,两铁环与小球都处于静止状态.现想办法使得两铁环间距离AB增大一些而同时仍能保持系统平衡,则OA绳和OB绳的拉力变化情况是( )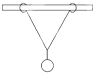 如图所示,在一根粗糙的水平直杆上套有两个质量均为m的铁环,两铁环上系着两根等长细线,共同拴住质量为M的小球,两铁环与小球组成的系统处于静止状态.现想办法使得两铁环间距离增大稍许而同时仍能保持系统平衡,则水平直杆对铁环的支持力FN和摩擦力Ff的可能变化是( )
如图所示,在一根粗糙的水平直杆上套有两个质量均为m的铁环,两铁环上系着两根等长细线,共同拴住质量为M的小球,两铁环与小球组成的系统处于静止状态.现想办法使得两铁环间距离增大稍许而同时仍能保持系统平衡,则水平直杆对铁环的支持力FN和摩擦力Ff的可能变化是( )

