题目内容
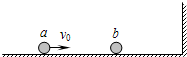 (2008?潮州二模)如图所示,光滑水平面上有两个质量分别为m1、m2的小球a、b,球a以水平速度vo=1m/s向右匀速运动,球b处于静止状态.两球右侧有一竖直墙壁,假设两球之间、球与墙壁之间发生正碰时均无机械能损失,为了使两球能发生、而且只能发生两次碰撞,试讨论两球的质量之比m1/m2应满足什么条件.
(2008?潮州二模)如图所示,光滑水平面上有两个质量分别为m1、m2的小球a、b,球a以水平速度vo=1m/s向右匀速运动,球b处于静止状态.两球右侧有一竖直墙壁,假设两球之间、球与墙壁之间发生正碰时均无机械能损失,为了使两球能发生、而且只能发生两次碰撞,试讨论两球的质量之比m1/m2应满足什么条件.分析:发生正碰,根据系统动量守恒和机械能守恒列出等式,根据m1、m2的大小关系进行讨论求解.
解答:解:设球a和球b第一次碰撞后速度分别为v1和v2,取向右为正方向.
由系统动量守恒:m1v0=m1v1+m2v2…①
系统机械能守恒得:
m1v02=
m1v12+
m2v22…②
解得:v1=
v2=
…③
讨论情况分别如下:
(1)、当m1>m2时,碰后a、b两球均向右运动,当球b与墙壁碰后以速度v2返回,并将与球a发生第二次碰撞,设碰后两球速度分别为v1′,v2′则有:
m1v1+m2(-v2)=m1v1′+m2v2′
m1v12+
m2v22=
m1v1′2+
m2v2′2
解得:v1′=
…④
v2′=
…⑤
因为m1>m2,故第二次碰后球b向右运动将再次与墙相碰,并以v2′返回;若要球a和球b不发生第三次碰撞,则应满足 v1′<0 且v2′≤|v'1|
即 (m1-m2)2-4m1m2<0 且4m1(m1-m2)≤|(m1-m2)2-4m1m2|…⑥
解得:3-2
<
<3+2
且1-
≤
≤1+
…⑦
再加上条件m1>m2 得:1<
≤1+
…⑧
(2)、m1=m2时,由①②得v1=0,v2=1m/s球b与墙壁碰后以速度1m/s返回与球a第二次碰撞,碰后a球以1m/s的速度向左运动,b球静止,此后两球不再相碰…⑨
(3)、m1<m2时,由①②可知v1<0,v2>0,即a球向左运动,球b向右运动并与墙壁碰后原速弹回,要使球b与球a发生第二次碰撞,应满足:
v2>-v1 即:2m1>-(m1-m2),得
>
…⑩
因m1<m2,故两球第二次相碰后,球a向左运动的速度必大于球b向左的运动速度,此后两球不再发生碰撞.
综合(1)(2)(3)得
满足范围:
<
≤1+
…
答:两球的质量满足范围:
<
≤1+
.
由系统动量守恒:m1v0=m1v1+m2v2…①
系统机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v1=
| m1-m2 |
| m1+m2 |
| 2m1 |
| m1+m2 |
讨论情况分别如下:
(1)、当m1>m2时,碰后a、b两球均向右运动,当球b与墙壁碰后以速度v2返回,并将与球a发生第二次碰撞,设碰后两球速度分别为v1′,v2′则有:
m1v1+m2(-v2)=m1v1′+m2v2′
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v1′=
| (m1-m2)2-4m1m2 |
| (m1+m2)2 |
v2′=
| 4m1(m1-m2) |
| (m1+m2)2 |
因为m1>m2,故第二次碰后球b向右运动将再次与墙相碰,并以v2′返回;若要球a和球b不发生第三次碰撞,则应满足 v1′<0 且v2′≤|v'1|
即 (m1-m2)2-4m1m2<0 且4m1(m1-m2)≤|(m1-m2)2-4m1m2|…⑥
解得:3-2
| 2 |
| m1 |
| m2 |
| 2 |
2
| ||
| 5 |
| m1 |
| m2 |
2
| ||
| 5 |
再加上条件m1>m2 得:1<
| m1 |
| m2 |
2
| ||
| 5 |
(2)、m1=m2时,由①②得v1=0,v2=1m/s球b与墙壁碰后以速度1m/s返回与球a第二次碰撞,碰后a球以1m/s的速度向左运动,b球静止,此后两球不再相碰…⑨
(3)、m1<m2时,由①②可知v1<0,v2>0,即a球向左运动,球b向右运动并与墙壁碰后原速弹回,要使球b与球a发生第二次碰撞,应满足:
v2>-v1 即:2m1>-(m1-m2),得
| m1 |
| m2 |
| 1 |
| 3 |
因m1<m2,故两球第二次相碰后,球a向左运动的速度必大于球b向左的运动速度,此后两球不再发生碰撞.
综合(1)(2)(3)得
| m1 |
| m2 |
| 1 |
| 3 |
| m1 |
| m2 |
2
| ||
| 5 |
答:两球的质量满足范围:
| 1 |
| 3 |
| m1 |
| m2 |
2
| ||
| 5 |
点评:解答本题的突破口是根据质量关系讨论碰后速度大小关系,本题很好的将直线运动问题与动量守恒和功能关系联系起来,比较全面的考查了基础知识.

练习册系列答案
相关题目
 (2008?潮州二模)在建筑工地上有时需要将一些建筑材料由高处送到低处,为此工人们设计了一种如图所示的简易滑轨:两根圆柱形木杆AB和CD相互平行,斜靠在竖直墙壁上,把一摞瓦放在两木杆构成的滑轨上,瓦将沿滑轨滑到低处.在实际操作中发现瓦滑到底端时速度较大,有可能摔碎,为了防止瓦被损坏,下列措施中可行的是( )
(2008?潮州二模)在建筑工地上有时需要将一些建筑材料由高处送到低处,为此工人们设计了一种如图所示的简易滑轨:两根圆柱形木杆AB和CD相互平行,斜靠在竖直墙壁上,把一摞瓦放在两木杆构成的滑轨上,瓦将沿滑轨滑到低处.在实际操作中发现瓦滑到底端时速度较大,有可能摔碎,为了防止瓦被损坏,下列措施中可行的是( ) (2008?潮州二模)内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为
(2008?潮州二模)内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为
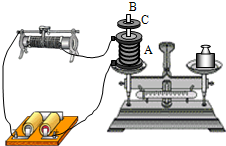 (2008?潮州二模)如图,A为螺线管,B为铁芯,C为套在铁芯B上的绝缘磁环,现将A、B、C放置在天平的左盘上,当A中通有电流I时,C悬停在A的上方,天平保持平衡;当调节滑动变阻器,使A中的电流增大时,绝缘磁环C将向上运动,在绝缘磁环C上升到最高点的过程中,若不考虑摩擦及空气阻力的影响,下列说法中正确的是( )
(2008?潮州二模)如图,A为螺线管,B为铁芯,C为套在铁芯B上的绝缘磁环,现将A、B、C放置在天平的左盘上,当A中通有电流I时,C悬停在A的上方,天平保持平衡;当调节滑动变阻器,使A中的电流增大时,绝缘磁环C将向上运动,在绝缘磁环C上升到最高点的过程中,若不考虑摩擦及空气阻力的影响,下列说法中正确的是( )