题目内容
11.若在某行星和地球上相对于各自的水平地面附近相同的高度处、以相同的速率平抛一物体,它们在水平方向运动的距离之比为2:$\sqrt{7}$.已知该行星质量约为地球的7倍,地球的半径为R.由此可知,该行星的半径约为( )| A. | $\frac{1}{2}$R | B. | $\frac{7}{2}$R | C. | 2R | D. | $\frac{\sqrt{7}}{2}$R |
分析 通过平抛运动的规律求出在星球上该行星表面的重力加速度与地球表面的重力加速度之比.再由万有引力等于重力,求出行星的半径.
解答 解:对于任一行星,设其表面重力加速度为g.
根据平抛运动的规律得 h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}$
则水平射程x=v0t=v0$\sqrt{\frac{2h}{g}}$.
可得该行星表面的重力加速度与地球表面的重力加速度之比 $\frac{{g}_{行}}{{g}_{地}}$=$\frac{{x}_{地}^{2}}{{x}_{行}^{2}}$=$\frac{7}{4}$
根据G$\frac{Mm}{{r}^{2}}$=mg,得g=$\frac{GM}{{r}^{2}}$
可得 $\frac{{g}_{行}}{{g}_{地}}$=$\frac{{M}_{行}}{{M}_{地}}$•$\frac{{R}_{地}^{2}}{{R}_{行}^{2}}$
解得行星的半径 R行=R地$\sqrt{\frac{{g}_{地}}{{g}_{行}}}$•$\sqrt{\frac{{M}_{行}}{{M}_{地}}}$=R×$\sqrt{\frac{4}{7}}$•$\sqrt{7}$=2R
故选:C.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,以及掌握万有引力等于重力这一理论,并能灵活运用.

练习册系列答案
相关题目
1.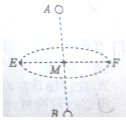 如图所示,真空中有两个点电荷A、B所带电荷量相等,M是其连线的中点,以M为圆心做一个圆,圆所在的平面与两点电荷的连线垂直,EF是该圆的一条直径,下列说法正确的是( )
如图所示,真空中有两个点电荷A、B所带电荷量相等,M是其连线的中点,以M为圆心做一个圆,圆所在的平面与两点电荷的连线垂直,EF是该圆的一条直径,下列说法正确的是( )
 如图所示,真空中有两个点电荷A、B所带电荷量相等,M是其连线的中点,以M为圆心做一个圆,圆所在的平面与两点电荷的连线垂直,EF是该圆的一条直径,下列说法正确的是( )
如图所示,真空中有两个点电荷A、B所带电荷量相等,M是其连线的中点,以M为圆心做一个圆,圆所在的平面与两点电荷的连线垂直,EF是该圆的一条直径,下列说法正确的是( )| A. | 如果A、B带同种电荷,E、M、F三点的场强相同 | |
| B. | 如果A、B带异种电荷,AB连线上,M点的场强最大 | |
| C. | 无论A、B带异种电荷还是同种电荷,图中圆都是等势线 | |
| D. | 如果A、B带同种电荷,仅在电场力的作用下,试探电荷有可能以图中圆为轨迹作匀速圆周运动 |
1.下列仪器不是利用涡流工作的有( )
| A. | 电磁炉 | B. | 微波炉 | C. | 金属探测器 | D. | 真空冶炼炉 |
 一质量为0.5kg的小物块放在水平地面上的A点,距离A点5m的位置B处是一面墙,如图所示,物块以v0=9m/s的初速度从A点沿AB方向运动,在与墙壁碰撞前瞬间的速度为7m/s,碰后以6m/s的速度反向运动直至静止.g取10m/s2.
一质量为0.5kg的小物块放在水平地面上的A点,距离A点5m的位置B处是一面墙,如图所示,物块以v0=9m/s的初速度从A点沿AB方向运动,在与墙壁碰撞前瞬间的速度为7m/s,碰后以6m/s的速度反向运动直至静止.g取10m/s2. 下暴雨时,有时会发生山体滑坡或泥石流等地质灾害.某地有一倾角为θ=37°(sin37°=$\frac{3}{5}$)的山坡C,上面有一质量为m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示.假设某次暴雨中,A浸透雨水后总质量也为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为$\frac{3}{8}$,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动,此时刻为计时起点;在第2s末,B的上表面突然变为光滑,μ2保持不变.已知A开始运动时,A离B下边缘的距离l=27m,C足够长,设最大静摩擦力等于滑动摩擦力.取重力加速度大小g=10m/s2.求:
下暴雨时,有时会发生山体滑坡或泥石流等地质灾害.某地有一倾角为θ=37°(sin37°=$\frac{3}{5}$)的山坡C,上面有一质量为m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图所示.假设某次暴雨中,A浸透雨水后总质量也为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为$\frac{3}{8}$,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动,此时刻为计时起点;在第2s末,B的上表面突然变为光滑,μ2保持不变.已知A开始运动时,A离B下边缘的距离l=27m,C足够长,设最大静摩擦力等于滑动摩擦力.取重力加速度大小g=10m/s2.求: 如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径.两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场.间距为d的两平行金属极板间有一匀强电场,上级板开有一小孔.一质量为m,电量为+q的粒子由小孔下方$\frac{d}{2}$处静止释放,加速后粒子以竖直向上的速度v射出电场,由H点紧靠大圆内侧射入磁场.不计粒子的重力.
如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径.两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场.间距为d的两平行金属极板间有一匀强电场,上级板开有一小孔.一质量为m,电量为+q的粒子由小孔下方$\frac{d}{2}$处静止释放,加速后粒子以竖直向上的速度v射出电场,由H点紧靠大圆内侧射入磁场.不计粒子的重力.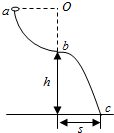 如图,位于竖直平面内的光滑轨道由四分之一圆弧ab和抛物线bc组成,圆弧半径Oa水平,b点为抛物线顶点.已知h=2m,s=$\sqrt{2}$m.取重力加速度大小g=10m/s2.
如图,位于竖直平面内的光滑轨道由四分之一圆弧ab和抛物线bc组成,圆弧半径Oa水平,b点为抛物线顶点.已知h=2m,s=$\sqrt{2}$m.取重力加速度大小g=10m/s2. 如图,三个质量相同的滑块A、B、C,间隔相等地静置于同一水平直轨道上.现给滑块A向右的初速度v0,一段时间后A与B发生碰撞,碰后A、B分别以$\frac{1}{8}$v0、$\frac{3}{4}$v0的速度向右运动,B再与C发生碰撞,碰后B、C粘在一起向右运动.滑块A、B与轨道间的动摩擦因数为同一恒定值.两次碰撞时间均极短.求B、C碰后瞬间共同速度的大小.
如图,三个质量相同的滑块A、B、C,间隔相等地静置于同一水平直轨道上.现给滑块A向右的初速度v0,一段时间后A与B发生碰撞,碰后A、B分别以$\frac{1}{8}$v0、$\frac{3}{4}$v0的速度向右运动,B再与C发生碰撞,碰后B、C粘在一起向右运动.滑块A、B与轨道间的动摩擦因数为同一恒定值.两次碰撞时间均极短.求B、C碰后瞬间共同速度的大小.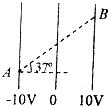 如图所示,某匀强电场中三个等势面及其对应的电势值,若A、B两点间的距离是2.5cm,则该匀强电场的场强大小为多少?
如图所示,某匀强电场中三个等势面及其对应的电势值,若A、B两点间的距离是2.5cm,则该匀强电场的场强大小为多少?