题目内容
【题目】如图所示,一根U型细管ABCD被固定在水平桌面上,其中,AB部分为水平光滑直管道,BC部分为半径为R=0.8m的水平光滑半圆管道,CD部分为长L=1.6m、动摩擦因数μ=0.5的水平直管道,管内一个直径略小于细管内径的小球被固定在A端的击发装置击出后以水平初速度v0沿AB做直线运动,接着进入BC做圆周运动,然后进入CD做直线运动,最后从紧靠桌子边缘的D端飞出落在水平地面的E点,已知,小球质量m=0.5kg,D点与水平地面间的距离为h=0.8m,D点与E点间的水平距离为x=3.2m,小球视为质点,不计空气阻力和直管与弯管衔接处的速度损失,π取3,g取10m/s2。求:
(1)小球从D点飞出时的速度vD的大小;
(2)小球在半圆形管道中运动时细管对小球的作用力F的大小;
(3)小球从B点运动到E点的时间t。(计算结果可保留根号)

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)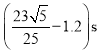 。
。
【解析】
本题考察多段运动分析,主要运用牛顿第二定律,平抛运动和圆周运动的基本性质。小球沿AB做匀速直线运动,接着进入BC做圆周运动,接着进入CD做匀减速直线运动,最后从D端飞出做平抛运动落在水平地面的E点。
(1)分析平抛运动
![]() ,
,![]()
解得
![]() ,
,![]()
(2)分析CD段,根据牛顿第二定律
![]()
![]()
解得
![]()
BC段做匀速圆周运动,细管对小球的作用力F充当向心力
![]()
(3)分析BC,CD,DE三段运动
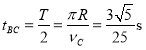
![]()
故总时间
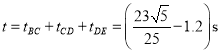

练习册系列答案
相关题目