��Ŀ����
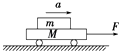
����Ŀ����ͼ��ʾ�������Ϊ�ȵ�б���ϣ����ʵ���һ��б��˹̶�����һ��������ΪM��ƽ��A���ӣ�һ������Ϊm������B����ƽ����Ҳ⣬A��B��б��Ķ�Ħ��������Ϊ�̣���ʼʱ���ְ�ס����Bʹ���ɴ���ѹ��״̬���ַ��֣�ʹA��Bһ����б�������˶�����Lʱ��A��B�ﵽ����ٶ�v��������˵����ȷ���ǣ�������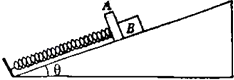
A.A��B�ﵽ����ٶ�vʱ����������Ȼ����
B.���˶�������A��B�ܹ����룬��A��Bǡ�÷���ʱ�������ٶȴ�С��Ϊg�� sin��+��cos�� ��
C.���ͷŵ�A��B�ﵽ����ٶ�v�Ĺ����У����ɶ�A�����Ĺ����� ![]() Mv2+MgLsin��+��MgLcos��
Mv2+MgLsin��+��MgLcos��
D.���ͷŵ�A��B�ﵽ����ٶ�v�Ĺ����У�B�ܵ��ĺ����������Ĺ����� ![]() mv2
mv2
���𰸡�B,D
���������⣺A��A��B�ﵽ����ٶ�vʱ��A��B�ļ��ٶ�Ӧ��Ϊ�㣮
��AB���壺��ƽ������֪
kx����m+M��gsin�ȩ��̣�m+M��gcos��=0��
���Դ�ʱ���ɴ���ѹ��״̬��A���������⣮
B��A��Bǡ�÷���ʱ��AB��ĵ���Ϊ0����B������������ţ�ٵڶ�����֪��
��б�淽��mgsin��+��mgcos��=ma��
��a=gsin��+��gcos�ȣ�
��ţ�ٵڶ�����֪��A��B�ļ��ٶ���ͬ��B�������⣮
C�����ͷŵ�A��B�ﵽ����ٶ�v�Ĺ����У�����AB���壬���ݶ��ܶ�����
����m+M��gLsin�ȩ��̣�m+M��gcos��L+W��= ![]() ��m+M��v2
��m+M��v2
���ɶ�A�����Ĺ�W��= ![]() ��m+M��v2+��m+M��gLsin��+�̣�m+M��gcos��L��C���������⣮
��m+M��v2+��m+M��gLsin��+�̣�m+M��gcos��L��C���������⣮
D�����ͷŵ�A��B�ﵽ����ٶ�v�Ĺ����У�����B�����ݶ��ܶ�����
B�ܵ��ĺ����������Ĺ�W��=��Ek= ![]() ��D�������⣮
��D�������⣮
�ʴ�Ϊ��BD��
����ؼ�����������������ֱ���˶�������ٶ�һ������ڼ��ٶ�Ϊ��ʱ�̣�AB�ٶ����ʱ����Ӧ�ļ��ٶ�Ϊ�㣬�����ɵĵ���ǡ����AB������б��ķ�����AB�ܵ��Ļ���Ħ����ƽ�⣮A��Bǡ�÷���ʱ��AB��ĵ���Ϊ0��A��B���й�ͬ�ļ��ٶȣ����ͷŵ�A��B�ﵽ����ٶ�v�Ĺ����У����ݶ��ܶ�����ⵯ�ɶ�A�����Ĺ������ͷŵ�A��B�ﵽ����ٶ�v�Ĺ����У�����B�����ݶ��ܶ������B�ܵ��ĺ����������Ĺ���

 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д� �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�