��Ŀ����
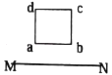
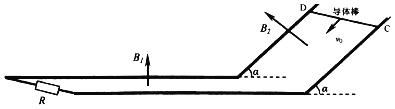
����Ŀ����ͼ��ʾ�������㹻���Ĺ⻬ƽ�н������죬���ˮƽ���Ҳ���б����ˮƽ����ƽ�����Ӳ�������30��нǣ���������ΪL��0.5m����˽��е���R��0.5����������費�ơ�ˮƽ���ֿռ�������ֱ���ϵ���ǿ�ų�B1��0.5T��б�沿���д�ֱ�ڵ���ƽ��б���ϵ���ǿ�ų�B2������Ϊm��0.2kg�ĵ����CD���뵼��Ӵ�������ʼ�մ�ֱ�ڵ��졣����CD��б�����µij��ٶ�v0��2m/s�������»�����ʱ���t��1s����ˮƽ���֡���g��10m/s2����
��1��B2�Ĵ�С��
��2������ˮƽ���ֺ�CD�ĵ�������Ͱ������������ٶȡ����ٶ������Ƕ����������CD����ˮƽ���ֺ���˶������
��3����CD�ӿ�ʼ������ֹͣ������R�ϲ���������Q��
��4����CD����ˮƽ����˲����ٶ�a�Ĵ�С�ͷ�����Ҫ�ð�����ˮƽ���ֺ��ٶȱ��ֲ��䣬���ڰ��ϼ�һ��ˮƽ����F��ֱ�����뿪ˮƽ�棬�Ӱ�����ˮƽ���ֿ�ʼ��ʱ����д����F��ʱ��t�ı���ʽ��������F�ķ���t��ȡֵ��Χ��
���𰸡���1��1T ��2������������ٶȼ�С�ļ����˶���ֱ��������ٶ�Ϊ��Ϊֹ ��3��2.4J ��4��![]() ����ˮƽ���ң�0��t��3.2s
����ˮƽ���ң�0��t��3.2s
��������
��1������������»�����ƽ��״̬����ƽ��������������Ÿ�Ӧǿ�ȡ�
��2�������ֶ�������д�����Ӧ�������������ֶ�������жϳ�����������Ӧ��ţ�ٵڶ�����������ٶȣ�Ȼ�������������˶��������˶����ʡ�
��3��Ӧ�������غ㶨���������R�ϲ����Ľ����ȡ�
��4����ţ�ٵڶ�����������ٶȴ�С��Ӧ��ţ�ٵڶ��������������
��1��������»������ܵ��İ�������F������B2IL��![]() ��
��
����������˶�����ƽ�������ã�mgsin����![]() ��
��
�������ݽ�ã�B2��1T��
��2�������ֶ����֪�����������CD�ĵ�����C����D�������ֶ����֪����������ܰ�������ˮƽ���ң���������ܺ�������ˮƽ���ң����ٶȷ������ң�������ٶ���������������˶�����ţ�ٵڶ����ɵã�![]() ��ma��
��ma��
���ٶȣ�a��![]() ���ٶ�v��С�����ٶ�a��С������������ٶȼ�С�ļ����˶���ֱ��������ٶ�Ϊ��Ϊֹ��
���ٶ�v��С�����ٶ�a��С������������ٶȼ�С�ļ����˶���ֱ��������ٶ�Ϊ��Ϊֹ��
��3�����������̣��������غ㶨�ɵã�Q��mgh+![]() ��
��
�������ݽ�ã�Q��2.4J��
��4�����������ˮƽ����˲�䣬
���ٶȣ�![]() ��
��
�������ݽ�ã�a��1.25m/s2������ˮƽ���ң�
��������ٶȲ��䣬��������ȼ���ֱ���˶���������ٶȣ�v��v0��at��
�Ե��������ţ�ٵڶ����ɵã�F+![]() ��ma��
��ma��
�������ݽ�ã�������F��![]() t ����ˮƽ���ң�
t ����ˮƽ���ң�
�Ӱ�����ˮƽ�濪ʼ�����뿪Ϊֹ�������������ȼ���ֱ���˶����ٶ�Ϊ�㣬Ȼ���������ȼ����˶�����������λ��Ϊ�㣬���ȱ����˶���λ�ƹ�ʽ�ã�s��v0t+![]() at2���������ݽ�ã�t��3.2s����0��t��3.2s��
at2���������ݽ�ã�t��3.2s����0��t��3.2s��