��Ŀ����
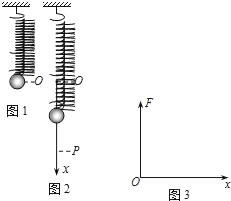
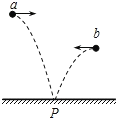
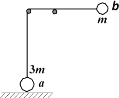
����Ŀ����ͼ��ʾ��һ�������쳤���������˸�ϵһ��С�� a �� b�����������̶���ͬһ�߶ȵĹ⻬ˮƽϸ���ϣ��� ��Ϊ 3m �� a �����ڵ����ϣ�����Ϊ m �� b ���ˮƽλ�þ�ֹ�ͷš��� a ��Ե���ѹ���պ�Ϊ��ʱ��b ��ڹ��ĽǶ�Ϊ �������н�����ȷ������ ��
A. ��=60
B. ��=90
C. b ��ڶ�����͵�Ĺ����У�������С�������Ĺ�����������С
D. b ��ڶ�����͵�Ĺ����У�������С�������Ĺ���һֱ����
���𰸡�BC
��������
����С��a��ֹ������С��b�°ڵ���͵�Ĺ�����ֻ��������������е���غ㣬�����͵��ٶȣ��ٸ�����������ʽ��ţ�ٵڶ�������ʽ����ϸ�ߵ�����������������˲ʱ���ʣ����Ը���P=Fvcos�ȷ���
����С��a��ֹ������С��b�°ڵ���͵�Ĺ����У���е���غ㣬��mgR=![]() mv2������͵㣬��F-mg=m
mv2������͵㣬��F-mg=m![]() ��������ã�F=3mg����aС��һֱ���־�ֹ�������������С��b�ڵ���͵�ʱ��С��aǡ�öԵ���ѹ������A����B��ȷ��С��b�����½����̣��ٶ��������ļнDz��ϱ�տ�ʼ���ٶ�Ϊ�㣬�ʹ���Ϊ�㣬����������ٶȴ�ֱ���ʹ���ҲΪ�㣬�ʹ����ȱ����С����C��ȷ��D����ѡBC��
��������ã�F=3mg����aС��һֱ���־�ֹ�������������С��b�ڵ���͵�ʱ��С��aǡ�öԵ���ѹ������A����B��ȷ��С��b�����½����̣��ٶ��������ļнDz��ϱ�տ�ʼ���ٶ�Ϊ�㣬�ʹ���Ϊ�㣬����������ٶȴ�ֱ���ʹ���ҲΪ�㣬�ʹ����ȱ����С����C��ȷ��D����ѡBC��

��ϰ��ϵ�д�
�����Ŀ