题目内容
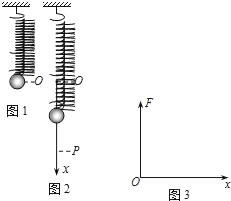
【题目】如图1所示，一根轻质弹簧上端固定在天花板上，下端挂一小球（可视为质点），弹簧处于原长时小球位于O点．将小球从O点由静止释放，小球沿竖直方向在OP之间做往复运动，如图2所示．小球运动过程中弹簧始终处于弹性限度内．不计空气阻力，重力加速度为g．
（1）在小球运动的过程中，经过某一位置A时动能为Ek1，重力势能为EP1，弹簧弹性势能为E弹1，经过另一位置B时动能为Ek2，重力势能为EP2，弹簧弹性势能为E弹2．请根据功是能量转化的量度，证明：小球由A运动到B 的过程中，小球、弹簧和地球组成的物体系统机械能守恒；
（2）已知弹簧劲度系数为k．以O点为坐标原点，竖直向下为x轴正方向，建立一维坐标系O﹣x，如图2所示．
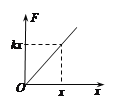
a．请在图3中画出小球从O运动到P的过程中，弹簧弹力的大小F随相对于O点的位移x变化的图象．根据F﹣x图象求：小球从O运动到任意位置x的过程中弹力所做的功W，以及小球在此位置时弹簧的弹性势能E弹；
b．已知小球质量为m．求小球经过OP中点时瞬时速度的大小v．
【答案】（1）略；（2）a.如图所示；
；
；b.
。
【解析】
试题（1）设重力做的功为WG，弹力做的功为W弹
根据动能定理 WG + W弹= Ek2 - Ek1（1分）
由重力做功与重力势能的关系 WG = Ep1 – Ep2（1分）
由弹力做功与弹性势能的关系 W弹= E弹1- E弹2（1分）
联立以上三式可得 Ek1+ Ep1+E弹1= Ek2+Ep2+E弹2 （1分）
（2）a. F-x图象如右图所示 （1分）
图中的图线和x轴围成的面积表示功的大小
所以弹力做功为（注：没有负号扣1分） （2分）
由弹力做功与弹性势能的关系 W弹=" 0" -E弹
解得（1分）
b. 小球由O点到OP中点，根据动能定理
（1分）
小球由O点到P点，根据机械能守恒定律
（1分）
解得（1分）
