题目内容
【题目】如图所示，质量m1＝1.0kg的物块随足够长的水平传送带一起匀速运动，传送带速度v0＝3.0m/s，质量m2＝4.0kg的物块在m1的右侧L＝2.5m处无初速放上传送带，两物块与传送带间的动摩擦因数均为μ＝0.10，两物块碰后瞬间m1相对地面的速度方向不变，大小为1.0m/s，求：
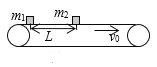
（1）质量为m2的物块释放后经过多少时间两物块相碰；
（2）碰撞后两物块间的最大距离。
【答案】(1) 
(2) 
【解析】(1)由牛顿第二定律可得碰撞前m2向右的加速度为: 
碰撞前运动时间内m1与m2位移关系为: 
,
即: 
代入数据计算得出: 
, 
(舍掉),
(2)碰前
随传送带匀速运动速度为
,碰前瞬间m2的速度
,
碰后瞬间
的速度为: 
规定向右为正方向,碰撞瞬间由动量守恒定律有: 
代入数据计算得出
碰后
和
均作匀加速运动至与传送带相对静止,因为
,其加速度均为a,
此过程中总有
均大于
的速度,故二者都相对传送带静止时距离最大,设为
相对滑动的时间为: 
相对滑动的时间为: 
相对滑动的时间内
先加速后匀速,则:
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
