题目内容
15.如图所示,有上下两层水平放置的平行导轨,两层导轨都足够长,电阻都不计.两导轨间距都是L=0.2m.上层导轨左端连接电阻R2=0.25Ω,下层导轨左端与电动势E=4v,内阻不计的电池及电阻R1=5Ω的电阻相串联.金属棒质量m=0.1kg置于下层导轨之上并与导轨垂直,可在导轨上滑动.下层导轨末端紧接着两根竖立在竖直平面内的半径为r=0.4m的绝缘材料做成的半圆形粗糙轨道.仅在上、下两层平行轨道所在区域里有一竖直向下的匀强磁场.当闭合电键K之后,金属棒由静止开始向右滑动最后成为匀速运动,滑过下层轨道后进入半圆形轨道,恰好可以通过半圆形轨道最高点以后滑入上层导轨.金属棒与下层轨道的动摩擦因数μ=0.1,上层轨道光滑,金属棒的电阻以及接触电阻匀不计,重力加速度g=10m/s2问:
(1)匀强磁场磁感应强度为多大时可使金属棒在通过半圆形轨道最低点时对轨道的压力最大.
(2)利用第1问的计算结果,求金属棒在通过半圆形轨道时因摩擦产生的内能大小.
(3)利用第1问的计算结果,求金属棒在上层轨道能滑行的距离及此过程中通过电阻R2的电荷量大小.
分析 (1)要使金属棒到达最低点时对轨道的压力最大,由共点力的平衡条件可得出对应的方程;再由数学规律可求出磁感应强度;
(2)在最高点处,重力充当向心力,上升过程由功能关系可求得因摩擦而产生的内能;
(3)对滑行过程由动量定理列式可求得电荷量;同理由动量定理可求得滑行的距离.
解答 解:(1)设杆的最大速度为vm
电路中的电流:
$I=\frac{{E-BL{v_m}}}{R_1}$
由共点力的平衡可知:
BIL=mgμ
即$({L^2}{v_m})•{B^2}-(L•E)•B+mgμ•R=0$
B有实数解△≥0
△=(L•E)2-4L2•vm•mgμR≥0
即${v_m}≤\frac{E^2}{4mgμ•R}=8m/s$
即$B=\frac{5}{4}T$
(2)最高点:$mg=m\frac{v^2}{r}\;\;\;\;\;v=\sqrt{gr}$
v=2m/s
上升过程:$\frac{1}{2}mv_m^2=\frac{1}{2}m{v^2}+mg•2r+{Q_f}$
即Qf=0.4J
(3)由动量定理可知:
0-mv=-BqL
$0-mv=-\frac{{{B^2}{L^2}}}{R_2}•{x_m}$
即q=$\frac{mv}{BL}$
解得:q=0.8C;
滑行距离:xm=$\frac{mv•{R}_{2}}{{B}^{2}{L}^{2}}$
解得:xm=0.8m
答:(1)匀强磁场磁感应强度为$\frac{5T}{4}$时可使金属棒在通过半圆形轨道最低点时对轨道的压力最大.
(2)利用第1问的计算结果,求金属棒在通过半圆形轨道时因摩擦产生的内能大小为0.4J;
(3)金属棒在上层轨道能滑行的距离为0.8m;此过程中通过电阻R2的电荷量大小为0.8C.
点评 本题考查感应电动势中的能量及受力关系,要注意正确应用常用的物理规律进行分析,如本题中采用了动量定理及功能关系进行分析.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 穿过导体框的磁通量为零的瞬间,线框中的感应电动势有可能很大 | |
| B. | 穿过导体框的磁通量越大,线框中感应电动势一定越大 | |
| C. | 穿过导体框的磁通量变化量越大,线框中感应电动势一定越大 | |
| D. | 穿过导体框的磁通量变化率越大,线框中感应电动势一定越大 |
 如图所示,质量m=2kg的重物用不可伸长的轻绳悬挂于天花板上的O点,一辆汽车在平台MN上通过固定在尾部的滑轮拖动重物,悬点O到平台的距离h=4m.开始时轻绳竖直,滑轮轻靠轻绳.汽车从N点以v=5m/s匀速向左运动,经过t=0.6s的时间到达M点,(不计一切摩擦、重力加速度g取10m/s2)以下判断正确的是( )
如图所示,质量m=2kg的重物用不可伸长的轻绳悬挂于天花板上的O点,一辆汽车在平台MN上通过固定在尾部的滑轮拖动重物,悬点O到平台的距离h=4m.开始时轻绳竖直,滑轮轻靠轻绳.汽车从N点以v=5m/s匀速向左运动,经过t=0.6s的时间到达M点,(不计一切摩擦、重力加速度g取10m/s2)以下判断正确的是( )| A. | 在此过程中重物沿直线运动 | |
| B. | 汽车到达M点时,重物的速度大小为3m/s | |
| C. | 汽车达到M点时,轻绳对物体的拉力大于20N | |
| D. | 在此过程中轻绳对重物做的功为54J |
 如图所示,A为地球赤道上的物体,B为地球同步卫星,C为地球表面上北纬60°的物体.已知A、B的质量相同.则下列关于A、B和C三个物体的说法中,正确的是( )
如图所示,A为地球赤道上的物体,B为地球同步卫星,C为地球表面上北纬60°的物体.已知A、B的质量相同.则下列关于A、B和C三个物体的说法中,正确的是( )| A. | A物体受到的万有引力小于B物体受到的万有引力 | |
| B. | B物体的向心加速度小于A物体的向心加速度 | |
| C. | A、B两物体的轨道半径的三次方与周期的二次方的比值相同 | |
| D. | A和B线速度的比值比C和B线速度的比值大,都小于1 |
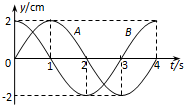 一列波长大于1m的横波沿着x轴正方向传播,处在x1=1m和x2=2m的两质点A、B的振动图象如图所示.由此可知( )
一列波长大于1m的横波沿着x轴正方向传播,处在x1=1m和x2=2m的两质点A、B的振动图象如图所示.由此可知( )| A. | 波长为$\frac{4}{3}$m | |
| B. | 波速为1m/s | |
| C. | 3s末A、B两质点的位移相同 | |
| D. | 1s末A点的振动速度小于B点的振动速度 |


 如图所示,一质量为m=1.5kg的滑块从倾角为θ=37°的斜面上自静止开始滑下,滑行距离s=10m后进入半径为R=9m的光滑圆弧AB,其圆心角θ,然后水平滑上与平台等高的小车.已知小车质量为M=3.5kg,滑块与斜面及小车表面的动摩擦因数μ=0.35,小车与地面光滑且足够长,取g=10m/s2.求
如图所示,一质量为m=1.5kg的滑块从倾角为θ=37°的斜面上自静止开始滑下,滑行距离s=10m后进入半径为R=9m的光滑圆弧AB,其圆心角θ,然后水平滑上与平台等高的小车.已知小车质量为M=3.5kg,滑块与斜面及小车表面的动摩擦因数μ=0.35,小车与地面光滑且足够长,取g=10m/s2.求