题目内容
5.如图1,在直角坐标系X≤0的区域存在磁感强度大小为2B0的匀强磁场,在X>0的区域存在如图2变化的匀强磁场,两磁场方向均垂直纸面向内,在t=0时刻有一质量为m,带电量为+q的带电粒子以大小为v0的初速度沿+X方向从O点进入磁场(不计粒子重力).
(1)求带电粒子在0~$\frac{πm}{q{B}_{0}}$时间内运动的半径和周期;
(2)试画出t=0时刻到t1=$\frac{17πm}{4q{B}_{0}}$时刻粒子的轨迹,并求出t1时刻粒子坐标位置及速度方向;
(3)若在t1=$\frac{17πm}{4q{B}_{0}}$时刻,撤去X>0区域处磁场,同时在该区域加一沿+Y方向匀强电场,请通过计算判断粒子再次进入电场前能否回到O点.
分析 (1)带电粒子进入磁场中由洛伦兹力提供向心力,由牛顿第二定律和圆周运动的规律可求其运动半径和周期.
(2)粒子在磁场中做匀速圆周运动,根据时间与周期的关系,画出粒子的运动轨迹,由几何关系求t1时刻粒子坐标位置,并分析速度方向.
(3)加匀强电场后,粒子在电场中做类平抛运动,由几何知识求出粒子再次进电场前在Y轴上的侧移量,与粒子轨迹半径比较,即可作出判断.
解答 解:(1)带电粒子在0~$\frac{πm}{q{B}_{0}}$时间内,由$q{v_0}(2{B_0})=\frac{mv_0^2}{r_1}$得 ${r_1}=\frac{{m{v_0}}}{{2q{B_0}}}$
周期${T_1}=\frac{{2π{r_1}}}{v_0}$ 得 ${T_1}=\frac{πm}{{q{B_0}}}$;
(2)当B=B0时 ${r_2}=\frac{{m{v_0}}}{{q{B_0}}}=2{r_1}$,${T_2}=\frac{2πm}{{q{B_0}}}$=2T1;
0~$\frac{πm}{q{B}_{0}}$的运动以r1为半径一个圆周,$\frac{πm}{q{B}_{0}}$~$\frac{2πm}{q{B}_{0}}$的运动以r2为半径半个圆周,$\frac{2πm}{q{B}_{0}}$~$\frac{3πm}{q{B}_{0}}$的运动以r1为半径一个圆周,$\frac{3πm}{q{B}_{0}}$~$\frac{7πm}{2q{B}_{0}}$的运动以r1为半径半个圆周,$\frac{7πm}{2q{B}_{0}}$~$\frac{4πm}{q{B}_{0}}$的运动以r2为半径$\frac{1}{4}$圆周,$\frac{4πm}{q{B}_{0}}$~$\frac{17πm}{4q{B}_{0}}$的运动以r1为半径$\frac{1}{4}$圆周,轨迹如下图所示.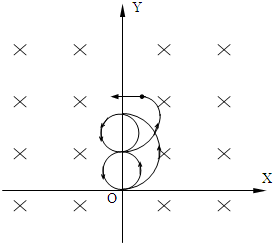
故坐标为($\frac{m{v}_{0}}{2q{B}_{0}}$,$\frac{5m{v}_{0}}{2q{B}_{0}}$),速度方向沿-X方向.
(3)如下图,设粒子进左侧磁场时速度与+Y成θ角,则再次进电场前在Y轴上的侧移量为△Y=2rsinθ
而 r=$\frac{m{v}_{0}}{2q{B}_{0}}$
得△Y=$\frac{mvsinθ}{q{B}_{0}}$=$\frac{m{v}_{0}}{q{B}_{0}}$<$\frac{5m{v}_{0}}{2q{B}_{0}}$
故不可能回到O点.
答:
(1)带电粒子在0~$\frac{πm}{q{B}_{0}}$时间内运动的半径为$\frac{m{v}_{0}}{2q{B}_{0}}$,周期为$\frac{πm}{q{B}_{0}}$;
(2)画出t=0时刻到t1=$\frac{17πm}{4q{B}_{0}}$时刻粒子的轨迹如图,t1时刻粒子坐标为($\frac{m{v}_{0}}{2q{B}_{0}}$,$\frac{5m{v}_{0}}{2q{B}_{0}}$),速度方向沿-X方向;
(3)粒子再次进入电场前不能回到O点.
点评 解决本题的关键是根据粒子的运动情况,画出其运动轨迹,要边计算,边分析,分析时要抓住圆周运动的周期性和对称性,结合几何知识求解.

| A. | 一定是匀强电场 | B. | 可能是一个点电荷形成的 | ||
| C. | 可能是两个等量异种点电荷形成的 | D. | 可能是两个等量同种点电荷形成的 |
 如图所示,图甲中M为一电动机,当滑动变阻器R的触头从左端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表读数在0.2A以下时,电动机没有发生转动.不考虑电表对电路的影响,以下判断正确的是( )
如图所示,图甲中M为一电动机,当滑动变阻器R的触头从左端滑到另一端的过程中,两电压表的读数随电流表读数的变化情况如图乙所示.已知电流表读数在0.2A以下时,电动机没有发生转动.不考虑电表对电路的影响,以下判断正确的是( )| A. | 电路中电源电动势为3.6V | |
| B. | 变阻器向右滑动时,V2读数逐渐减小 | |
| C. | 此电路中,电动机的输出功率减小 | |
| D. | 变阻器的最大阻值为30Ω |
| A. | 加速上升 | B. | 减速上升 | C. | 加速下降 | D. | 减速下降 |
 如图所示,传送带与地面成夹角a=30°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5㎏的物体,它与传送带间的动摩擦因数μ=0.6,已知传送带从A→B的长度L=16m,则物体从A到B需要的时间为多少?
如图所示,传送带与地面成夹角a=30°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5㎏的物体,它与传送带间的动摩擦因数μ=0.6,已知传送带从A→B的长度L=16m,则物体从A到B需要的时间为多少? 一带电质点的质量为m,电量为q,以平行于 Ox 轴的速度v从y轴上的a点射入第一象限的区域,如图所示.为了使该质点能从x轴上的b点以垂直于x轴的速度 v 射出,可在适当的地方加一个垂直于xoy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,则此圆形磁场区域的最小面积为$\frac{π{m}^{2}{v}^{2}}{2{B}^{2}{q}^{2}}$.(重力忽略不计)
一带电质点的质量为m,电量为q,以平行于 Ox 轴的速度v从y轴上的a点射入第一象限的区域,如图所示.为了使该质点能从x轴上的b点以垂直于x轴的速度 v 射出,可在适当的地方加一个垂直于xoy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,则此圆形磁场区域的最小面积为$\frac{π{m}^{2}{v}^{2}}{2{B}^{2}{q}^{2}}$.(重力忽略不计) 如图所示,在坐标系xOy的第一象限内,有平行于y轴向上的匀强电场,在第四象限内有垂直于纸面向外的匀强磁场,在y轴上A、B两点各有一个粒子源,A、B两点到坐标原点的距离和x轴上一点C到坐标原点的距离相等,两粒子源沿x轴正向同时发射出速度大小分别为v1、v2的两个粒子,粒子的质量、电量大小相等,电性相同,不计粒子的重力,两粒子都从C点第一次穿过x轴.
如图所示,在坐标系xOy的第一象限内,有平行于y轴向上的匀强电场,在第四象限内有垂直于纸面向外的匀强磁场,在y轴上A、B两点各有一个粒子源,A、B两点到坐标原点的距离和x轴上一点C到坐标原点的距离相等,两粒子源沿x轴正向同时发射出速度大小分别为v1、v2的两个粒子,粒子的质量、电量大小相等,电性相同,不计粒子的重力,两粒子都从C点第一次穿过x轴.