题目内容
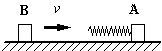
在光滑水平面上静止放置一长木板B,B的质量为M=2kg,B右端离竖直墙5m,
现有一小物体A,其质量为m=1kg,以v0=6m/s的速度从B的左端水平滑上B,如图所示,A与B间的动摩擦因数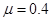 ,在运动过程中只是B与墙壁碰撞,碰撞时间极短,且碰撞时无能量损失,取g=10m/s2,求:要使A最终不脱离B,木板B的最短长度是多少?
,在运动过程中只是B与墙壁碰撞,碰撞时间极短,且碰撞时无能量损失,取g=10m/s2,求:要使A最终不脱离B,木板B的最短长度是多少?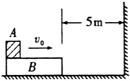
现有一小物体A,其质量为m=1kg,以v0=6m/s的速度从B的左端水平滑上B,如图所示,A与B间的动摩擦因数
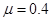 ,在运动过程中只是B与墙壁碰撞,碰撞时间极短,且碰撞时无能量损失,取g=10m/s2,求:要使A最终不脱离B,木板B的最短长度是多少?
,在运动过程中只是B与墙壁碰撞,碰撞时间极短,且碰撞时无能量损失,取g=10m/s2,求:要使A最终不脱离B,木板B的最短长度是多少?
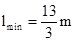
试题分析:
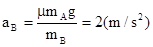
若达到共同速度(M+m)V共=mVo ∴V共=(m/s)
∵2aBS>V
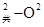 ∴碰前已达共同速度
∴碰前已达共同速度在碰后返回的过程中 (M+m)V
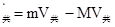
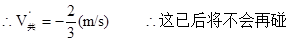
∵碰中无能量损失
∴ZW=△Ek
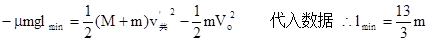
点评:解决本题的关键是A与B组成的系统在碰撞过程中满足动量守恒,B在运动过程中遵循牛顿第二定律,A在B上滑动时,A相对于B滑动的位移为相对位移,摩擦力在相对位移上做的功等于系统机械能的损耗.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目