题目内容
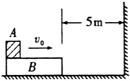
(12分)如图5-14所示,有两个物体A,B,紧靠着放在光滑水平桌面上,A的质量为2kg,B的质量为3kg。有一颗质量为100g的子弹以800m/s的水平速度射入A,经过0.01s又射入物体B,最后停在B中,A对子弹的阻力为3×103N,求A,B最终的速度。

vA=6m/s,vB=21.94m/s
试题分析:设A,B质量分别为mA,mB,子弹质量为m。子弹离开A的速度为了v,物体A,B最终速度分别为vA,vB。
在子弹穿过A的过程中,以A,B为整体,以子弹初速v0为正方向,应用动量定理。
f·t=(mA+mB)u (u为A,B的共同速度)
解得:u=6m/s。
由于B离开A后A水平方向不受外力,所以A最终速度VA=u=6m/s。
对子弹,A和B组成的系统,应用动量守恒定律:
mv0=mA·vA+(m+mB)vB
解得:vB=21.94m/s。
物体A,B的最终速度为vA=6m/s,vB=21.94m/s。
点评:本题考查了在碰撞过程中的动量守恒定律。在运用时要注意是否满足动量守恒定律的条件,从而列示求解。

练习册系列答案
相关题目
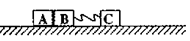
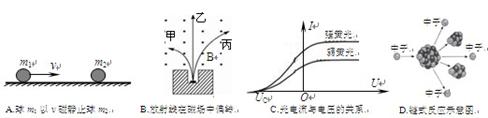
 粒子流,具有很强的穿透能力
粒子流,具有很强的穿透能力
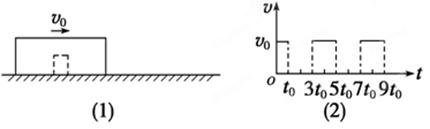
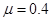 ,在运动过程中只是B与墙壁碰撞,碰撞时间极短,且碰撞时无能量损失,取g=10m/s2,求:要使A最终不脱离B,木板B的最短长度是多少?
,在运动过程中只是B与墙壁碰撞,碰撞时间极短,且碰撞时无能量损失,取g=10m/s2,求:要使A最终不脱离B,木板B的最短长度是多少?