题目内容
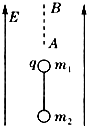如图所示，质量为m1、带有正电荷q的金属小球和质量为m2不带电的小木球之间用绝缘细线相连后，置于竖直向上、场强为E、范围足够大的匀强电场中，两球恰能以速度v匀速竖直上升，当小木球运动到A点时细线突然断裂，小木球运动到B点时速度为零，则（ ）| A、小木球的速度为零时，金属小球的速度也为零 | ||
B、小木球的速度为零时，金属小球的速度大小为
| ||
C、A、B两点之间的电势差为
| ||
| D、小木球从A到B的过程中，其动能的减少量等于两球重力势能的增加量 |
分析：线断开前，两球在电场中做匀速直线运动，两球的总重力与电场力平衡，断开细线后，两球的总重力与电场力均不变，合力为零，两球组成的系统总动量守恒，根据动量守恒定律分析小木球的速度为零时，金属小球的速度．对于木球B，细线断开后，只受重力，机械能守恒，由机械能守恒定律求解上升的高度AB，再由U=Ed求出A、B间的电势差．根据能量守恒定律分析小木球从点A到点B的过程中，其动能的减少量与两球重力势能的增加量的关系．
解答：解：A、B断开细线后，两球组成的系统合力为零，总动量守恒，根据动量守恒定律得，（m1+m2）v=m2v′得，金属小球的速度大小为v′=
．故A错误，B错误；
C、断开细线后，木球的机械能守恒，则有m2gh=
m2v2，得h=
，即A、B间距离为h=
，两点A、B之间的电势差为U=Eh=
．故C正确；
D、小木球从点A到点B的过程中，其动能的减少量等于木球重力势能的增加量．故D错误．
故选：C．
| (m1+m2)v |
| m1 |
C、断开细线后，木球的机械能守恒，则有m2gh=
| 1 |
| 2 |
| v2 |
| 2g |
| v2 |
| 2g |
| Ev2 |
| 2g |
D、小木球从点A到点B的过程中，其动能的减少量等于木球重力势能的增加量．故D错误．
故选：C．
点评：本题在物理上称为脱钩问题，两球没有发生作用，但系统的合力为零，也遵守动量守恒．
练习册系列答案
寒假学与练系列答案
相关题目
如图所示，质量为m1的物体甲通过三段轻绳悬挂，三段轻绳的结点为O．轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连，轻绳OA与竖直方向的夹角θ=37°，物体甲、乙均处于静止状态．（已知：sin37°=0.6，cos37°=0.8）求：
如图所示，质量为m1=10g的子弹以800m/s的速度向右射向放在光滑地面上静止的质量为2kg的物块．
如图所示，质量为m1=2.0kg、长为L=10.0m的平板小车，静止在光滑水平地面上，一质量为m2=0.5kg的小物块以v0=10.0m/s速度从左端冲上平板车，已知小物块与平板车之间的动摩擦因数μ=0.30．有关平板车和小物块最后的速度v'1和v'2的大小，以及整个过程中系统内能的增加量Q的计算试，正确的是（g=10m/s2）（ ）A、v′1=v′2=
| ||||||
B、v′1=v′2=
| ||||||
C、v′1＜
| ||||||
D、v′1＜
|
（2011?河南模拟）如图所示，质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行，长木板保持静止状态．已知木块与长木板间的动摩擦因数为μ1，长木板与水平地面间的动摩擦因数为μ2，则（ ）
（2009?崇文区一模）如图所示，质量为m1=1kg的小物块P置于桌面上的A点并与弹簧的右端接触（不拴接），轻弹簧左端固定，且处于原长状态．质量M=3.5kg、长L=1.2m的小车静置于光滑水平面上，其上表面与水平桌面相平，且紧靠桌子右端．小车左端放有一质量m2=0.5kg的小滑块Q．现用水平向左的推力将P缓慢推至B点（弹簧仍在弹性限度内）时，撤去推力，此后P沿桌面滑到桌子边缘C时速度为2m/s，并与小车左端的滑块Q相碰，最后Q停在小车的右端，物块P停在小车上距左端0.5m处．已知AB间距离L1=5cm，AC间距离L2=90cm，P与桌面间动摩擦因数μ1=0.4，P、Q与小车表面间的动摩擦因数μ2=0.1，（g取10m/s2），求：