Question

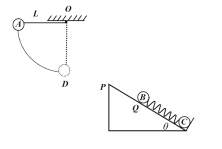
【题目】如图所示，固定在水平面上倾角θ＝37°的光滑斜面底端有一垂直于斜面的挡板，可看成质点的小球A、B、C质量均为m＝2kg，小球B、C通过一劲度系数k＝57.6N/m的轻质弹簧相连，初始时，球B、C处于静止状态，球A拴在绳长为L=0.8m一端，绳子的另一端固定在O点，将A拉到O点的等高处由静止释放，当球A运动到最低点时，绳子恰好断掉，球A被水平抛出，恰好无碰撞地由P点滑上斜面，继续运动xPQ=m后与静止于Q点的球B相碰，碰撞时间极短，碰后A、B粘在一起，已知不计空气阻力，重力加速度g＝10m/s2，sin37°＝0.6，cos37°＝0.8。求：

(1)绳子的最大承受拉力的大小Fm；

(2)碰撞前后损失的机械能；

(3)设从球A、B粘在一起到球C恰好离开挡板这一过程经历了时间t＝2s，则这一过程中弹簧对球AB的冲量大小I为多少？（弹簧始终处于弹性限度内）

Answer 1

【答案】(1)60N；(2)18J；(3)

【解析】

(1)到过程中

在点对小球

代入数据解得

(2)当球离开点后，球做平抛运动，达点时速度沿斜面向下，则点速度

从点到点的过程中，由动能定理得

代入数据解得

从A与B相碰到碰撞结束这一过程系统动量守恒，以A的初速度方向为正方向，由动量守恒定律得

代入数据解得

故碰撞后损失的机械能

(3)设在碰撞前弹簧的压缩量为，由平衡条件得

当C恰好离开挡板时，弹簧处于伸长状态，设伸长量为，对C，由平衡条件得

从A、B碰撞完到C恰好离开挡板，设此时A、B的共同速度为，从碰撞结束到C恰好离开挡板对系统由能量守恒

代入数据解得

从A、B碰撞完到C恰好离开挡板，设弹簧对A、B的冲量为，规定沿斜面向上为正方向，由动量定理得

代入数据解得，此过程弹簧对A、B的冲量大小